Предмет: Математика,
автор: palaver8
Сделать проверку матрицы по формуле А^-1*A=Е, если:
Приложения:
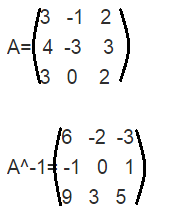
Ответы
Автор ответа:
0
У вас опечатка. В матрице A^(-1) в 3 строке должно быть -9.
Не обращая внимания на подчеркивания _, это для выравнивания строк.
(6 -2 -3)*(3 -1 2) = (6*3-2*4-3*3 __ 6(-1)-2(-3)-3*0 ___ 6*2-2*3-3*2)
(-1 0 1)*(4 -3 3) = (-1*3+0*4+1*3 _-1(-1)+0(-3)+0*1_ -1*2+0*3+1*2) =
(-9 3 5)*(3 0 2) = (-9*3+3*4+5*3 -9(-1)+3(-3)+5*0 _ -9*2+3*3+5*2)
= (18-8-9 ___ -6+6-0 ___ 12-6-6) = (1 0 0)
= (-3+0+3 ___1+0+0 ____-2+0+2) = (0 1 0) = Е
= (-27+12+15_ 9-9+0 _ -18+9+10) = (0 0 1)
Да, все правильно, получается единичная матрица.
Не обращая внимания на подчеркивания _, это для выравнивания строк.
(6 -2 -3)*(3 -1 2) = (6*3-2*4-3*3 __ 6(-1)-2(-3)-3*0 ___ 6*2-2*3-3*2)
(-1 0 1)*(4 -3 3) = (-1*3+0*4+1*3 _-1(-1)+0(-3)+0*1_ -1*2+0*3+1*2) =
(-9 3 5)*(3 0 2) = (-9*3+3*4+5*3 -9(-1)+3(-3)+5*0 _ -9*2+3*3+5*2)
= (18-8-9 ___ -6+6-0 ___ 12-6-6) = (1 0 0)
= (-3+0+3 ___1+0+0 ____-2+0+2) = (0 1 0) = Е
= (-27+12+15_ 9-9+0 _ -18+9+10) = (0 0 1)
Да, все правильно, получается единичная матрица.
Похожие вопросы
Предмет: Обществознание,
автор: Аноним
Предмет: Русский язык,
автор: ajsezimzusupova89
Предмет: Английский язык,
автор: Аноним
Предмет: Химия,
автор: malchik2694