Question

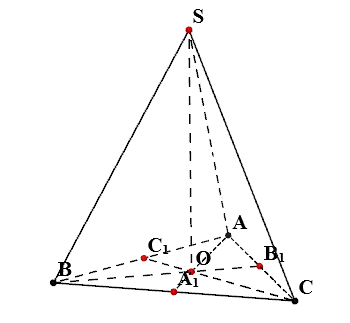
Правильная треугольная пирамида вписана в конус, образующая, которого равна 10 и имеет с плоскостью основания угол 60 градусов. Найти объем пирамиды.

Answer 1

Пирамида называется вписанной в конус, если ее ребра совпадают с образующими конуса, а основание вписано в основание конуса.

$V=frac{S*h}{3}$ - объем пирамиды

sin a = h ( высота пирамиды)/b (ребро пирамиды)

h=sina * b

h=sin60*10=0.866*10=8,66 - высота пирамиды

 

ОС^2=СS^2-SO^2

OC^2=10^2-8.66^2=100-75=25

OC=5

 

CC1=$frac{sqrt{3}*BC}{2}\ </var></p> <p><var>BC=frac{2*CC1}{sqrt{3}}$

 

CC1=2OC=10

 

BC=2*10/1.73=11.5

 

$S=frac{sqrt{3}*a}{4}$ площадь основания пирамиды.где а - сторона основания - ВС

 

S=230/4=57.5

 

$V=frac{S*h}{3}$

 

V=57.5*8.66=498

 

 

 Смотри вложение