Question

Доказать,что уравнение имеет единственный корень и найти его 5х-cos3x-5π=1

Answer 1

$5x-cos3x-5 pi =1 \ 5x-5 pi-1 =cos3x \ left { {{y_1=5x-5 pi -1} atop {y_2=cos3x}} right.$
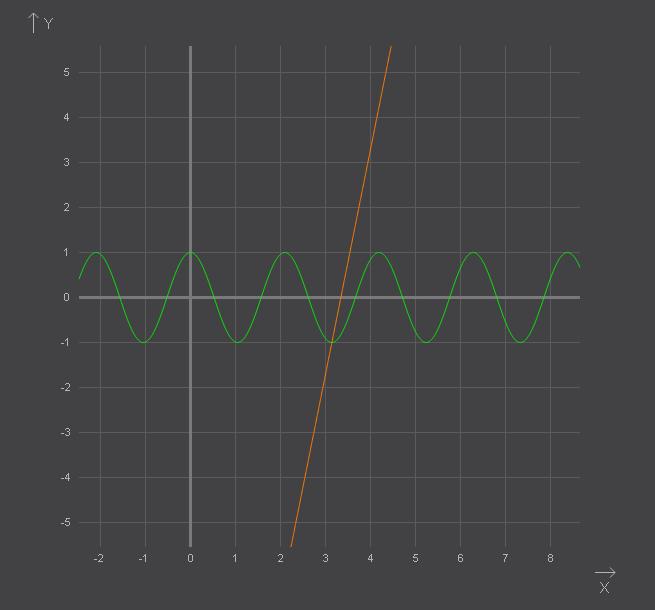
График функции y=5x-5π-1 представляет собой прямую у=х, растянутую в 5 раз от оси абсцисс и сдвинутую на (5π+1) единиц вниз.
График функции у=cos3x представляет собой косинусоиду у=cosх, сжатую в 3 раза к оси ординат.
Так как графики пересекаются в одной точке, то и исходное уравнение имеет только один корень. Абсцисса точки пересечения приближенно равна 3,1: предположим, что искомый корень равен π≈3,14 и выполним проверку:
$5 pi -cos3 pi -5 pi =1 \ -(-1) - =1 \ 1=1$
Получили верное равенство, значит число π - действительно корень уравнения.
Ответ: π