Предмет: Геометрия,
автор: rvasilisa99
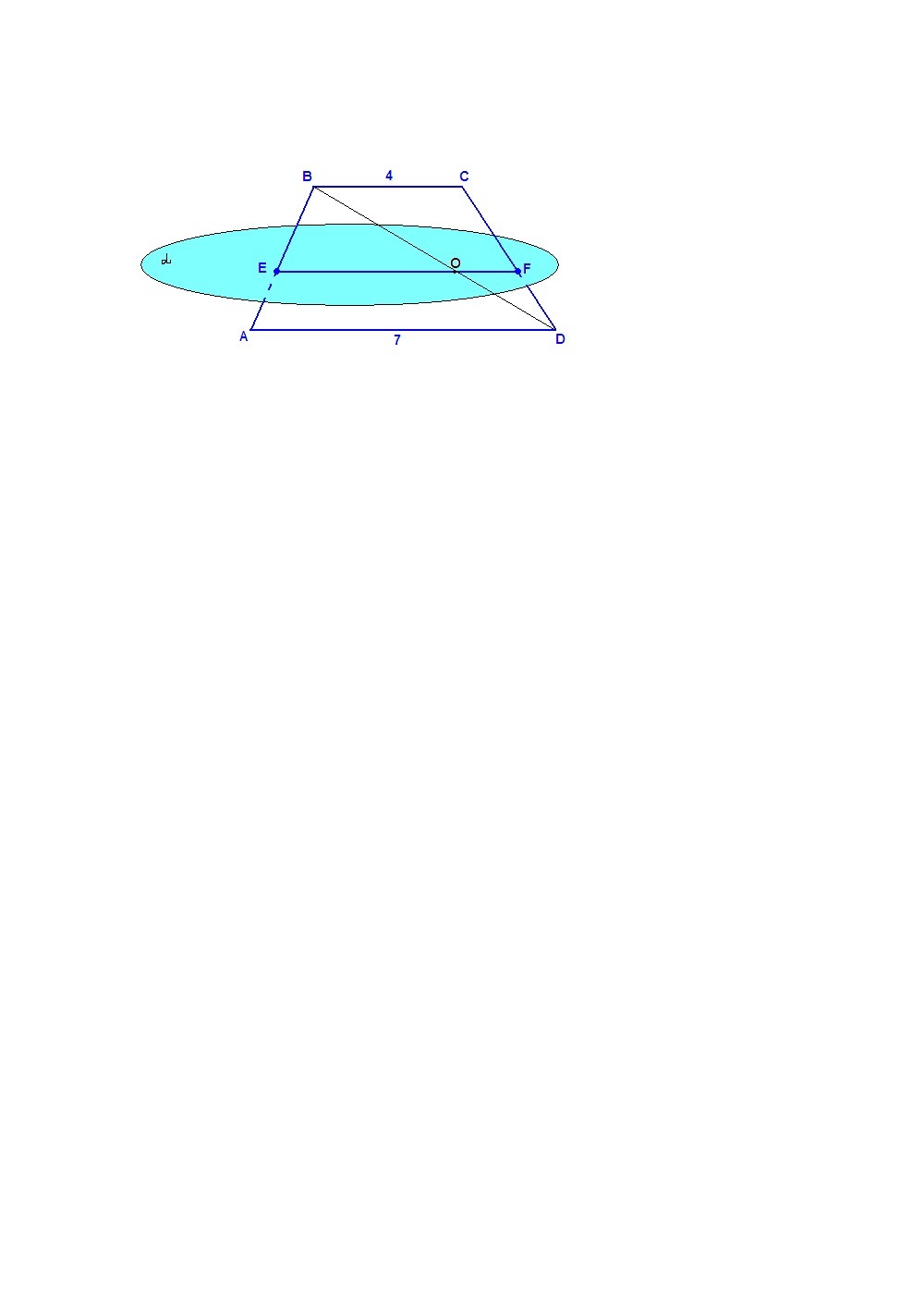
Плоскость пересекает стороны трапеции ABCD в точках E и F соответственно. Основания трапеции параллельны плоскости альфа и равны 4 см и 7 см. Найдите EF, если BE:EA=2:3
Ответы
Автор ответа:
0
ВС║α, плоскость трапеции проходит через ВС и пересекает α по прямой EF, значит EF║BC.
CF : FD = BE : EA = 2 : 3 по теореме Фалеса
Проведем диагональ BD, О - точка пересечения диагонали и EF.
ΔЕВО подобен ΔABD по двум углам (угол В общий, ∠ВЕО = ∠ВАD как соответственные при пересечении параллельных прямых EF и AD секущей АВ),
ЕО : AD= BE : BA = 2 : 5
EO = AD · 2 / 5 = 7 · 2 / 5 = 14/5 = 2,8 см
ΔDOF подобен ΔDBC по двум углам (угол D общий, ∠DOF = ∠DBC как соответственные при пересечении параллельных прямых EF и ВС секущей BD)
OF : BC = DF : DC = 3 : 5
OF = BC · 3 / 5 = 4 · 3 / 5 = 12/5 = 2,4 см
EF = EO + OF = 2,8 + 2,4 = 5,2 см
CF : FD = BE : EA = 2 : 3 по теореме Фалеса
Проведем диагональ BD, О - точка пересечения диагонали и EF.
ΔЕВО подобен ΔABD по двум углам (угол В общий, ∠ВЕО = ∠ВАD как соответственные при пересечении параллельных прямых EF и AD секущей АВ),
ЕО : AD= BE : BA = 2 : 5
EO = AD · 2 / 5 = 7 · 2 / 5 = 14/5 = 2,8 см
ΔDOF подобен ΔDBC по двум углам (угол D общий, ∠DOF = ∠DBC как соответственные при пересечении параллельных прямых EF и ВС секущей BD)
OF : BC = DF : DC = 3 : 5
OF = BC · 3 / 5 = 4 · 3 / 5 = 12/5 = 2,4 см
EF = EO + OF = 2,8 + 2,4 = 5,2 см
Приложения:
Похожие вопросы
Предмет: Биология,
автор: Andrei9786
Предмет: Оʻzbek tili,
автор: Muhammadyusuf9595
Предмет: Английский язык,
автор: Аноним
Предмет: Алгебра,
автор: rudykh96
Предмет: Математика,
автор: hannanov2000