Предмет: Алгебра,
автор: Owlonthewindow
Объясните, как решать, пожалуйста
Приложения:
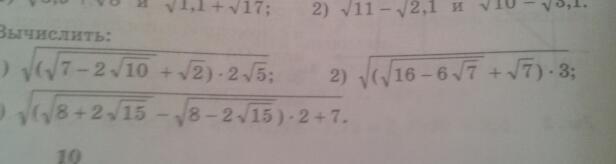
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: anenkoinnai15
Предмет: Русский язык,
автор: hadiatullomuminov
Предмет: Английский язык,
автор: bazhaevainara
Предмет: Математика,
автор: Полинаaaæ
Предмет: Алгебра,
автор: meri123456789