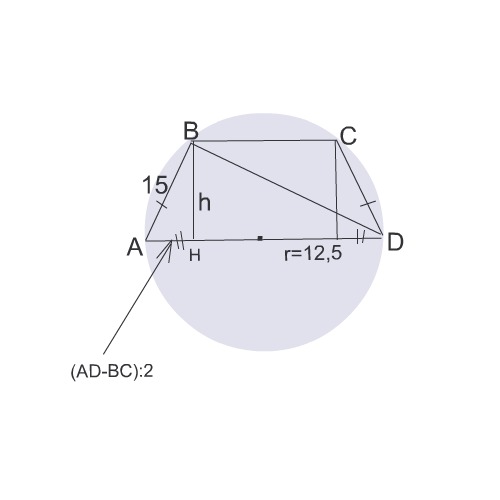
центр окружности описанной около трапеции лежит на ее большем основании. боковая сторона трапеции равна 15 радиус окружности 12.5. найдите площадь трапеции.
Ответы
Дана трапеция АВСD, вокруг которой описана окружность.
Около выпуклого четырёхугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180° (π радиан).
Из этого следует, что трапеция равнобедренная.
АВ=СD=15 см
Площадь трапеции равна произведению ее высоты на полусумму оснований.
Известно только одно основание - оно равно диаметру окружности
АD=2 r=25 cм
Так как центр описанной окружности лежит на большем основании трапеции,
диаметр окружности, ее боковая сторона и диагональ образуют прямоугольный треугольник с гипотенузой, равной диаметру.
Высоту трапеции h = ВD найдем по формуле высоты прямоугольного треугольника, проведенного из прямого угла к гипотенузе:
h = 2s/a , где а - гипотенуза.
Площадь треугольника пока не известна.
Для ее нахождения нужно найти длину второго катета -диагонали трапеции ВD.
ВD=√(АD²-АВ²)=√(25²-15²)=√400=20 см
2s ABD=АВ·ВD=15·20=300 cм²
h =300:25= 12 см
Отрезок от А до основания Н высоты ВН трапеции равен в равнобедренной трапеции полуразности оснований.
АН найдем из прямоугольного треугольника АВН по теореме Пифагора.
Полуразность оснований 9 см
Разность оснований 18 см
Меньшее основание
ВС= 25 -18=7 см
S трапеции = 12·(25+7):2 =192 см²