Question

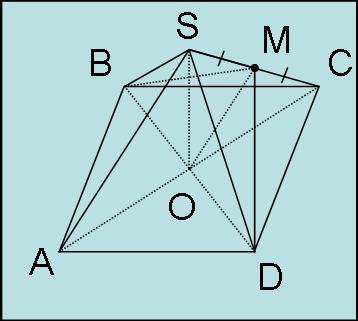
В четырехугольной пирамиде SABCD все ребра равны. Докажите, что плоскость BMD перпендикулярна прямой SC, где M - середина ребра SC

Answer 1

Надо доказать, что углы SMO и SMD прямые

 

Т.к. все ребра равны (путь a), то треугольник SCD - равносторонний значит DM является и медианой и высотой, т.е. угол DMS=90

 

Т.к. AB=AD=a то по т. Пифагора $BD=sqrt{AD^2+AB^2}=sqrt{a^2+a^2}=asqrt{2}$

Так же по т.Пифагора: $SO=sqrt{SD^2-OD^2}=sqrt{a^2-(frac{asqrt{2}}{2})^2}=sqrt{frac{2a^2}{4}}=frac{asqrt{2}}{2}$

Т.к. CO=OD=SO то треугольник SOC равнобедренный, ОМ - медина и высота то угол SMO=90