Question

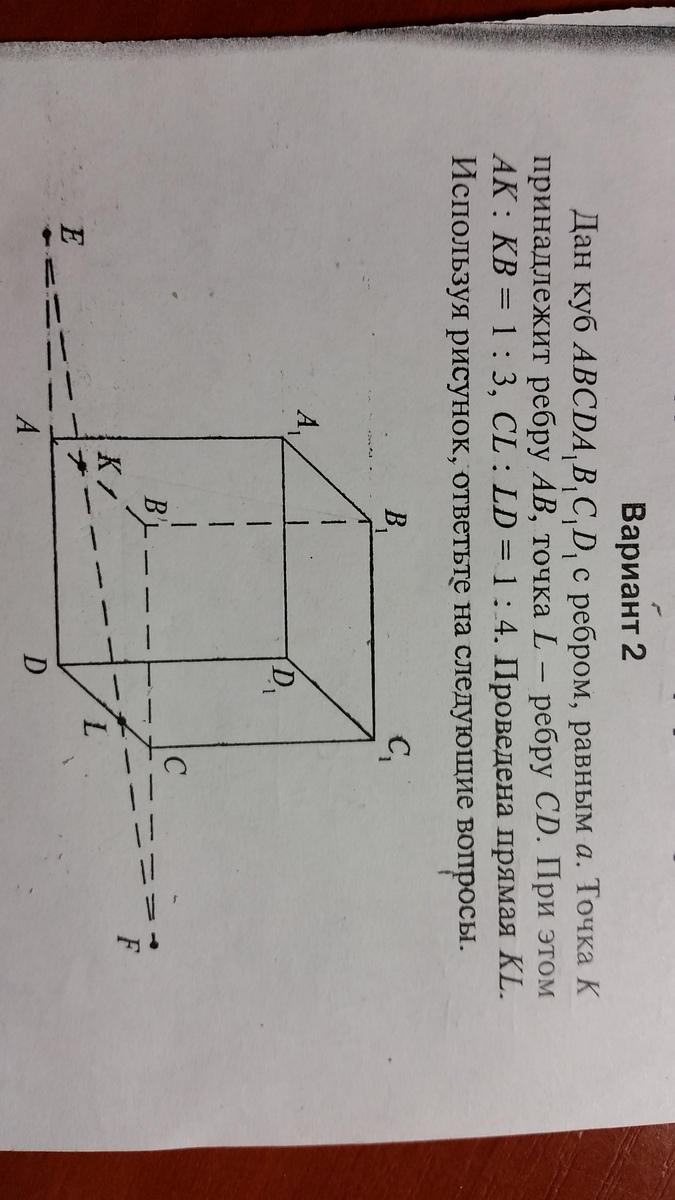
Помогите, пожалуйста, найти KL и EF

Answer 1

AKLD - прямоугольная трапеция, в которой AD = a, AK = a/4, LD = 4a/5.
KL - ее боковая сторона. Проведем высоту КР из точки К к стороне CD. Отрезок PL равен 4а/5 - а/4 = 11а/20.
Треугольник KPL - прямоугольный, с гипотенузой KL и катетами КР = а и PL = 11а/20. По теореме Пифагора:
KL = $sqrt{a^2 + (11a/20)^2} = a sqrt{521} /20$

Отрезок EF является

Answer 2

чуть-чуть недописано....

Answer 3

там можно из подобия дорешать

Answer 4

Почему-то не помещается полный ответ. Да, из подобия треугольников ELD и EKA с коэффициентом подобия 16:5 следует, что ЕА = 5а/11, и из прямоугольного треугольника ЕКА можем как гипотенузу найти ЕК. И аналогично - LF. А потом сложить три отрезка: EF = EK + KL + LF