Question

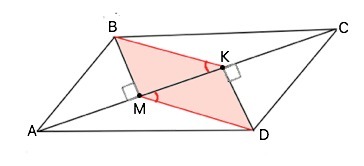
Из вершин B и D параллелограмма ABCD проведены перпендикуляры BM и DK к диагонали AC.Докажите,что четырехугольник BKDM-параллелограмм.
ОЧЕНЬ НУЖНОООоООО!!!

Answer 1

Диагональ параллелограмма делит его на два равных треугольника. 

По условию ВМ перпендикулярна АС и является высотой ∆ АВС. 

DK перпендикулярна АС и является высотой ∆ADC. В равных треугольниках высоты, проведенные из равных вершин, равны. ⇒

ВМ=KD

Треугольники ВМК=DMK  по двум катетам ( ВМ=KD из доказанного, МК - общий) Отсюда ВК=DM. 

Если противоположные стороны четырехугольника попарно равны, то этот четырехугольник ― параллелограмм. Ч.т.д.