Question

Геометрия 7 класс Задача: Угол 1 разделить на угол 2 равно угол 5 разделить на угол 4 найти угол 1 2 3 4

Answer 1

Правильное условие:
Дано: угол 1:углу 2=5:4
Найти: угол 1,угол 2,угол 3,угол 4.
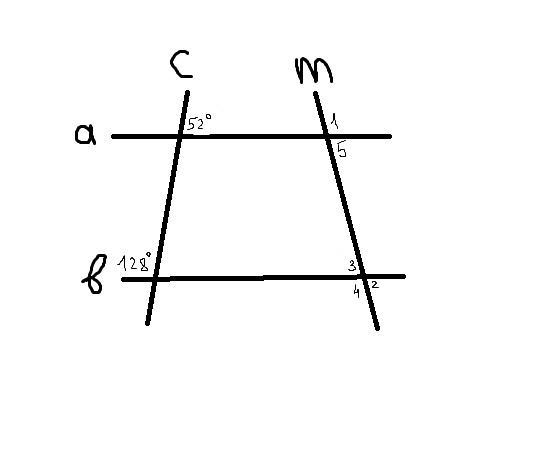
Рисунок из условия в приложении.
Решение: 
  Рассмотрим прямые а, в предположим, что прямая С секущая.
и если бы а,в были параллельные, то углы в 128* и смежный(нижний) угол с ∠52* назывались накрестлежащими(они равны)
180-52=128*
128*=128*(и)
Мы доказали параллельность прямых а и в.
Если мы рассмотрим эти же прямые с секущей М, то
1) У ∠1 есть вертикальный угол(они равны)
2) Найденный угол с ∠4 соответственные (они равны)
3) из пунктов 1 и 2 следует, что ∠1=∠4
4) углы 4 и 2 смежные (их сумма равна 180*)
5) из пунктов №3 и №4 делаем вывод, что ∠1+∠2=180*
Нам дано отношение найденных нами углов, и мы нашли их сумму, составляем уравнение:
∠1=5х
∠2=4х
5х+4х=180*
9х=180*
х=180/9
х=20
∠1=5*20=100*
∠2=4*20=80*
Теперь :
∠1=∠4  =100*( равенство мы ранее доказали)
∠3 =∠ 2  (вертикальные, 80*)
∠3=∠5 (накрест лежащие, 80*)