Предмет: Алгебра,
автор: Bergo
Объясните решение...
Приложения:
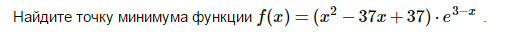
Ответы
Автор ответа:
0
Для начала найдём критические точки(возможные точки min или max). Для этого найдём производную и приравняем её к нулю:

Разделим всё уравнение на , т.к. при любых x оно больше нуля(по определению показательной функции):
, т.к. при любых x оно больше нуля(по определению показательной функции):

Корни можно находить или по Дискриминанту или по теореме Виета(с подбором значения). Я воспользуюсь т. Виета:
{x₁+x₂=39
{x₁·x₂=2*37
Легко заметить что это корни 2 и 37. Это и будут критические точки.
Теперь нужно кое-что вспомнить. Когда производная положительная - тогда возрастает функция, отрицательная - убывает. Если в точке производная меняет свой знак с отрицательной на положительную, то эта точка и является точкой минимума.
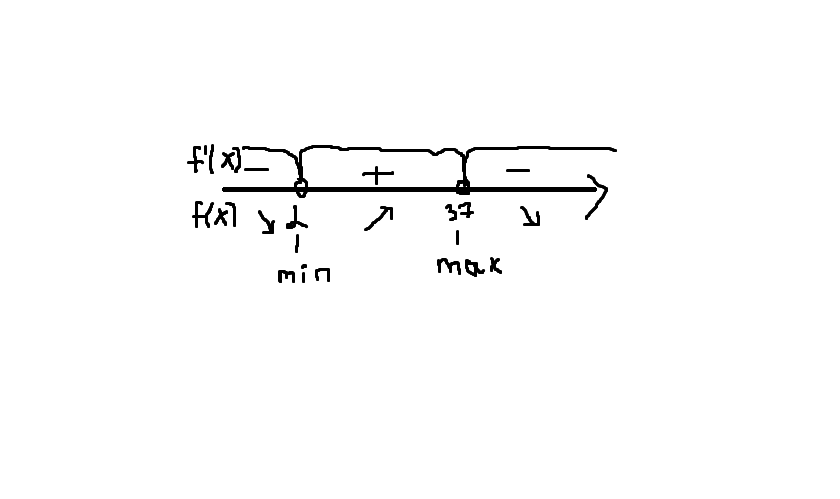
Определим знаки производной(с помощью метода интервалов) и сразу же найдём точку минимума.
Вложение.
x=2 - точка min
Разделим всё уравнение на
Корни можно находить или по Дискриминанту или по теореме Виета(с подбором значения). Я воспользуюсь т. Виета:
{x₁+x₂=39
{x₁·x₂=2*37
Легко заметить что это корни 2 и 37. Это и будут критические точки.
Теперь нужно кое-что вспомнить. Когда производная положительная - тогда возрастает функция, отрицательная - убывает. Если в точке производная меняет свой знак с отрицательной на положительную, то эта точка и является точкой минимума.
Определим знаки производной(с помощью метода интервалов) и сразу же найдём точку минимума.
Вложение.
x=2 - точка min
Приложения:
Автор ответа:
0
е в степени 3-х
Автор ответа:
0
оно всегда равно 1?
Автор ответа:
0
нет, оно равно равно единице только при x=3, но нам этого не нужно
Автор ответа:
0
нам нужно знать только то, что e^(3-x) не равно нулю, а значит оно не будет корнем уравнения, а значит мы можем разделить всё уравнение на e^(3-x)
Автор ответа:
0
а при делении число само на себя мы и получаем 1
Похожие вопросы
Предмет: Английский язык,
автор: mkiselev685
Предмет: География,
автор: nenenkonina2
Предмет: Другие предметы,
автор: nastuxxaa1139
Предмет: Литература,
автор: enny1992
Предмет: Алгебра,
автор: AnastasiyaKorban