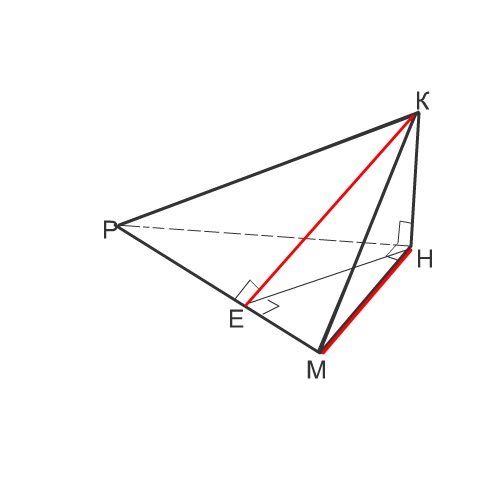
В основании тетраэдра MPHК лежит треугольник МРН с углом Н, равным 90 градусов. Прямая НК перпендикулярна плоскости основания. Найдите расстояние от точки К до прямой МР и расстояние от точки М до плоскости РНК, если КН=9см, НР=24см, угол МРН = 30 градусов.
Ответы
Делаем рисунок и по нему определяем, длину каких отрезков необходимо определить.
Расстояние от точки К до прямой МР - это высота КЕ грани КРМ.
Расстояние от точки М до плоскости РНК - катет МН основания, т.к. расстояние определяют перпендикуляром, а угол МНР - прямой.
Найдем гипотенузу РМ основания.
РМ=РН:cos( 30°)
РМ=24:( √3):2=48:√3
Умножим числитель и знаменатель на √3, чтобы избавиться от неудобной дроби:
48√3:√3·√3=48√3:3=16√3 см
МН=1/2 РМ, как катет, противолежащий углу 30°
МН=8√3 см
КЕ найдем из прямоугольного треугольника КЕН.
КН дана в условии.
ЕН противолежит углу 30° в прямоугольном треугольнике РНЕ, где НЕ и ЕР - катеты, а РН - гипотенуза.
ЕН=24:2=12 см
КЕ²=ЕН²+КН²=225
КЕ=15
Ответ: Расстояние от точки К до прямой МР равно 15 см.
Расстояние от точки М до плоскости РНК равно 8√3 см