1. Треугольник ABC- равнобедренный прямоугольный треугольник (угол C = 90○). Середины сторон AB, BC, CA обозначены соответственно точками D, E, F. Проведены отрезки DC, DE, DF. Докажите, что точка D будет на равном расстоянии от вершин данного треугольника.
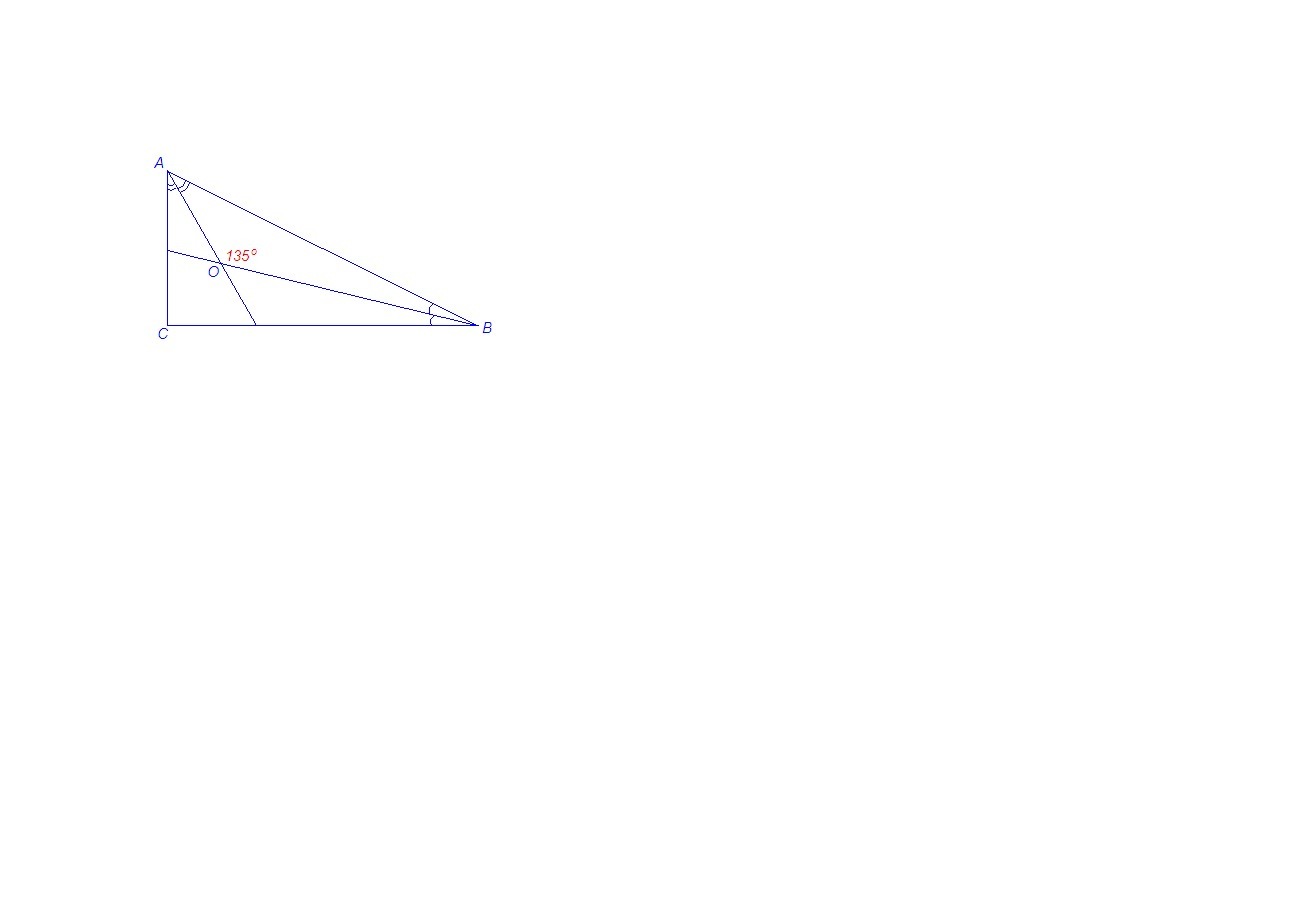
2. Задача. : Докажите, что угол между биссектрисами острых углов прямоугольного треугольника равен 145○.
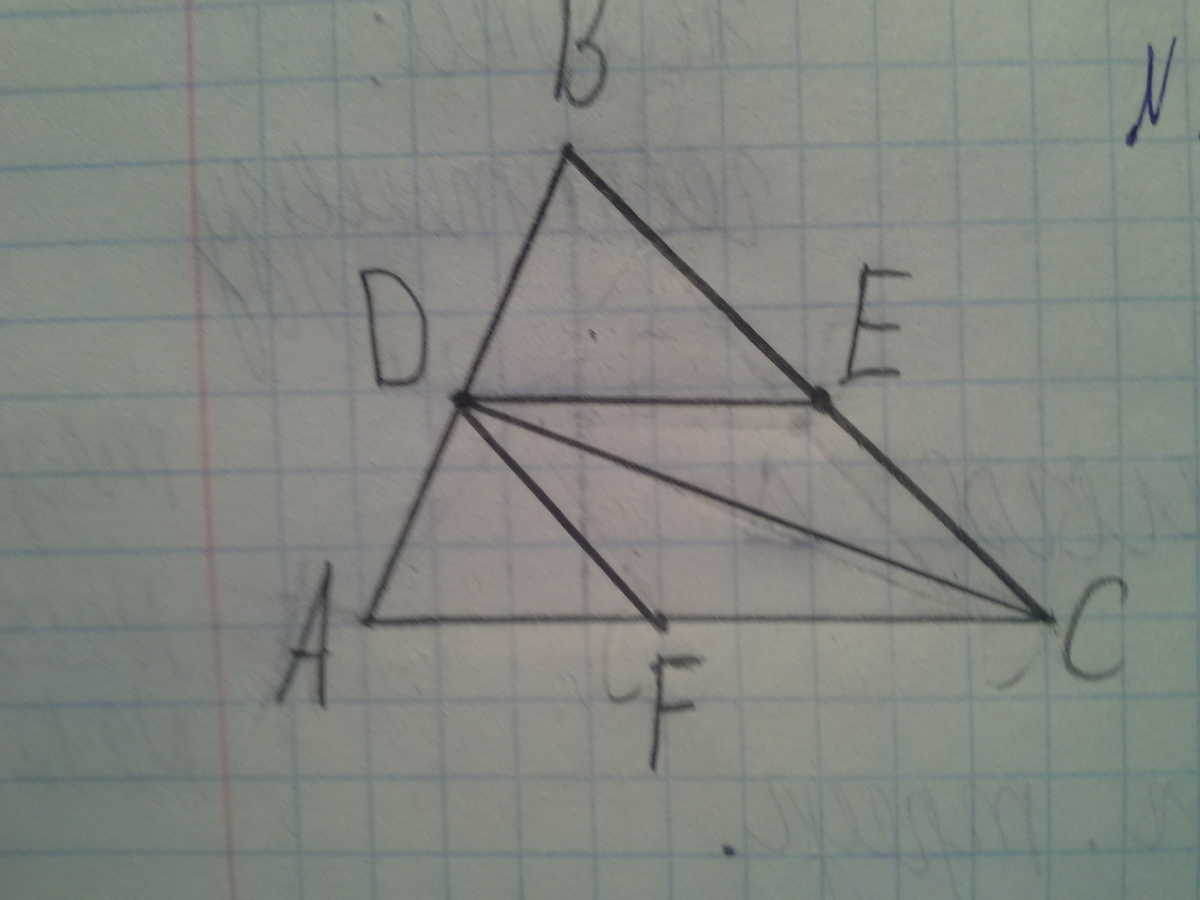
Ответы
Добавлено решение задачи 2
Т.к. треугольник АВС равнобедренный, то СД являющаяся по условию медианной (т. Д середина АВ), является и биссектрисой и высотой. Отсюда в треугольнике СДВ угол Д=90°, угол С = 90/2 = 45°° и
∠В = 180 - 90 - 45 = 45°. Т.к. угол ДCВ = углу СВД, то треугольник равнобедренный и СД=ВД. Аналогично рассматриваем треугольник АСD и получаем что АД = СД = ВД, что и требовалось доказать.
2. Сумма острых углов прямоугольного треугольника равна 90°. Тогда сумма их половинок равна 45°.∠АОВ = 180° - 45° = 135°.
Т.е. в условии задачи ошибка. Угол между биссектрисами острых углов прямоугольного треугольника равен 135°