Question

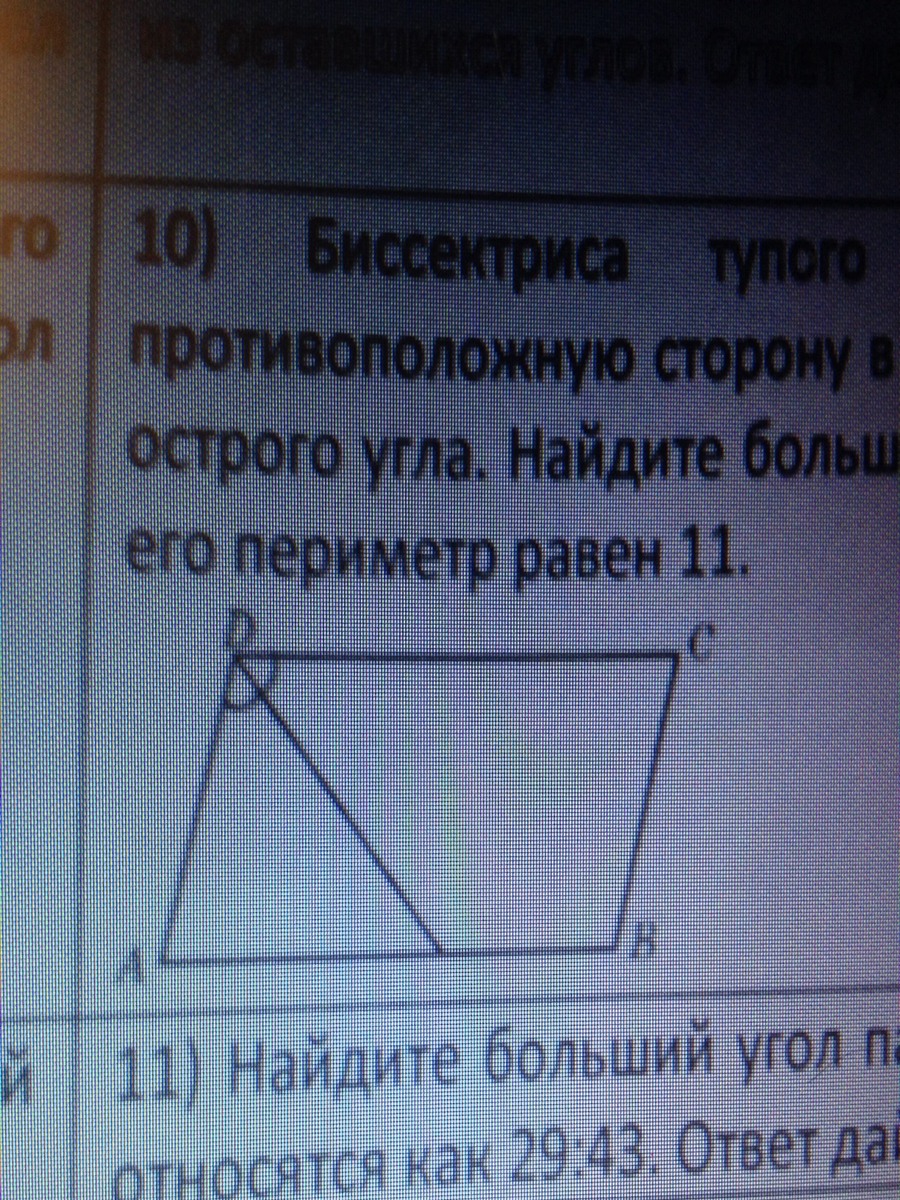
Биссектриса тупого угла параллерограмма делит противоположную сторону в отношении 3:4, считая от вершины острого угла. Найдите большую сторону параллелограмма,если его периметр равен 11

Answer 1

∠CDK = ∠DKA по свойству параллельных прямых и секущей. Так как Биссектриса DK Делит∠ADC пополам то ∠ADK=∠AKD и отсюда следует что ΔADK равнобедренный. Зная что $P_{ABCD} =2*(AB+BC)$ получаем 2*(AB+BC)=11 то AB+BC=5.5 
Из условия задачи сторона AB=3:4 то есть вся длинна 3+4=7(частям), а AD=3(частям) получаем 7+3=10 теперь 5,5 / 10(частей) =0,55 (одна часть)
Отсюда находим большую сторону 0,55*7=3,85
Ответ: 3,85