Question

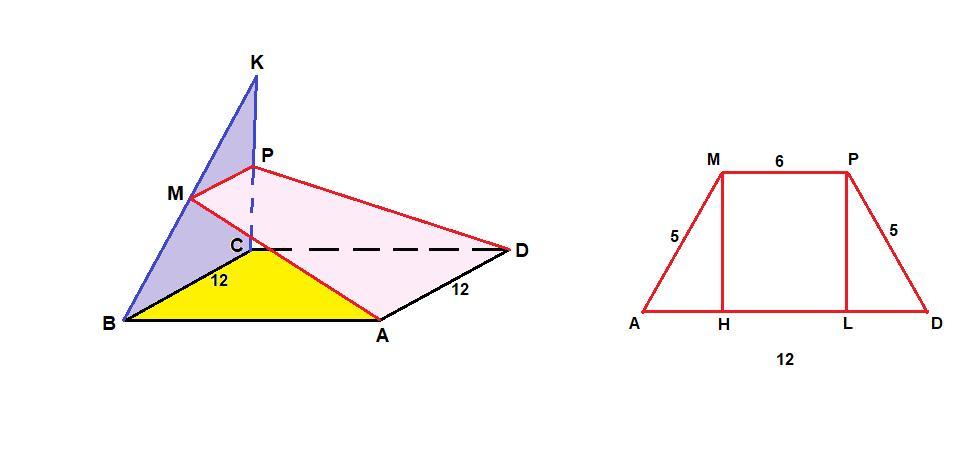
Квадрат ABCD и равнобедренный треугольник KBC(KB=BC) лежат в разных плоскостях. M и P -- середины отрезков BK и CK.
1) Определите вид четырехугольника MPDA.
2) Вычислите его площадь, если AB=12см, MA=PD=5см.

Answer 1

Ответ:

1)   MPDA - равнобедренная трапеция

2)    36 см²

Объяснение:

1) МР - средняя линия треугольника ВСК, поэтому

        МР║ВС и МР = 1/2 ВС = 6 см

МР║ВС, ВС║AD, ⇒ МР║AD.

Значит, MPDA трапеция. А так как МА = PD = 5 см, то

MPDA - равнобедренная трапеция.

2) Проведем высоты трапеции МН и PL. MPLH - прямоугольник, так как у него все углы прямые, тогда

HL = MP = 6 см.

ΔАМН = ΔDPL по гипотенузе и катету (∠АНМ = ∠DLP = 90°, так как проведены высоты, АМ = DP по условию и МН = PL как высоты), значит

АН = DL = (AD - HL)/2 = (12 - 6)/2 = 3 см

ΔАМН: прямоугольный, египетский, значит МН = 4 см.

Smpda = (MP + AD)/2 · MH = (6 + 12)/2 · 4 = 36 см²