Предмет: Математика,
автор: minshov
В квадрат площадью 24 вписан прямоугольник так, что на каждой стороне квадрата лежит одна вершина прямоугольника. Длины сторон прямоугольника относятся как 1:3. Найти площадь прямоугольника.
Ответы
Автор ответа:
0
Прямоугольник - параллелограмм.
Чтобы углы вписанного в квадрат параллелограмма были прямыми, его стороны должны быть параллельны диагоналям квадрата, которые пересекаются под прямым углом. Можно вписать параллелограмм с прямыми углами, стороны которого не параллельны диагоналям квадрата, но только если это квадрат.
Сделаем рисунок.
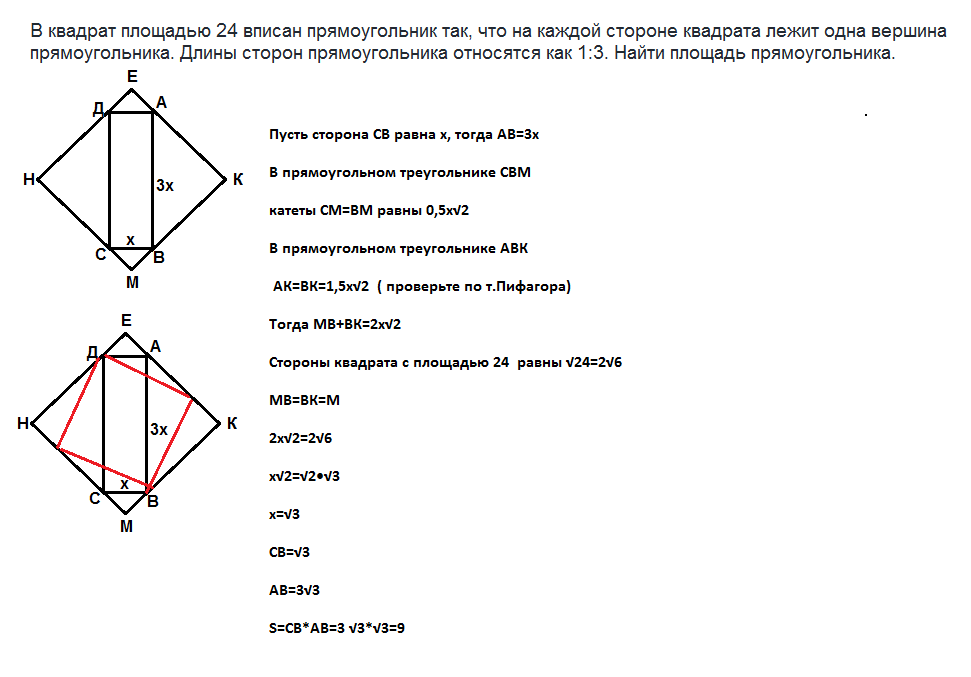
Обозначим вершины квадрата ЕКМН, вершины прямоугольника АВСД.
Пусть сторона СВ равна х, тогда АВ=3х
В прямоугольном треугольнике СВМ катеты СМ=ВМ равны 0,5х√2
В прямоугольном треугольнике АВК АК=ВК=1,5х√2 ( проверьте по т.Пифагора)
Тогда МК=МВ+ВК=2х√2
Стороны квадрата с площадью 24 равны √24=2√6
2х√2=2√6
x√2=х√2•√3
x=√3
CB=√3
AB=3√3
S (АВСД)=CB*AB=3 √3*√3=9
Чтобы углы вписанного в квадрат параллелограмма были прямыми, его стороны должны быть параллельны диагоналям квадрата, которые пересекаются под прямым углом. Можно вписать параллелограмм с прямыми углами, стороны которого не параллельны диагоналям квадрата, но только если это квадрат.
Сделаем рисунок.
Обозначим вершины квадрата ЕКМН, вершины прямоугольника АВСД.
Пусть сторона СВ равна х, тогда АВ=3х
В прямоугольном треугольнике СВМ катеты СМ=ВМ равны 0,5х√2
В прямоугольном треугольнике АВК АК=ВК=1,5х√2 ( проверьте по т.Пифагора)
Тогда МК=МВ+ВК=2х√2
Стороны квадрата с площадью 24 равны √24=2√6
2х√2=2√6
x√2=х√2•√3
x=√3
CB=√3
AB=3√3
S (АВСД)=CB*AB=3 √3*√3=9
Приложения:
Похожие вопросы
Предмет: Математика,
автор: boburjon058
Предмет: Химия,
автор: grigart772
Предмет: Алгебра,
автор: Lenfor
Предмет: Математика,
автор: sashaumnova11
Предмет: Математика,
автор: sashaumnova11