Предмет: Геометрия,
автор: Glonas2002
Конспект по теме сравнение углов.
Ответы
Автор ответа:
0
3. Сравнение углов
В данный момент рассмотрим равенство углов. В этой ситуации также имеется три случая:
1. Случай: (Рис. 4). Углы ∠AOB, ∠MQN равны Если луч MQ совпадает с лучом ОА, а луч QN совпадает с лучом ОВ, то углы ∠AOB, ∠MQN равны.2.
Случай: (Рис. 3.) Углы ∠AOB > ∠MQNЕсли луч MQ совпадает с лучом ОА, а луч QN не совпадает с лучом ОВ, а лежит во внутренней области угла ∠AOB, то ∠AOB > ∠MQN.3. Случай:( Рис. 2.) Углы ∠AOB < ∠MQNЛуч MQ совпадает с лучом ОА, а луч QN не совпадает с лучом ОВ, а лежит во внешней области угла ∠AOB, в таком случае ∠AOB < ∠MQN.
4. Биссектриса угла
Определение: Луч, который выходит из вершины угла и делит его пополам, называется биссектрисой.На рисунке 10 обозначена биссектриса ОМ угла ∠АОВ. Заметим, что, по определению, .
(Рис. 1). ОМ – биссектриса угла ∠AOB
В данный момент рассмотрим равенство углов. В этой ситуации также имеется три случая:
1. Случай: (Рис. 4). Углы ∠AOB, ∠MQN равны Если луч MQ совпадает с лучом ОА, а луч QN совпадает с лучом ОВ, то углы ∠AOB, ∠MQN равны.2.
Случай: (Рис. 3.) Углы ∠AOB > ∠MQNЕсли луч MQ совпадает с лучом ОА, а луч QN не совпадает с лучом ОВ, а лежит во внутренней области угла ∠AOB, то ∠AOB > ∠MQN.3. Случай:( Рис. 2.) Углы ∠AOB < ∠MQNЛуч MQ совпадает с лучом ОА, а луч QN не совпадает с лучом ОВ, а лежит во внешней области угла ∠AOB, в таком случае ∠AOB < ∠MQN.
4. Биссектриса угла
Определение: Луч, который выходит из вершины угла и делит его пополам, называется биссектрисой.На рисунке 10 обозначена биссектриса ОМ угла ∠АОВ. Заметим, что, по определению, .
(Рис. 1). ОМ – биссектриса угла ∠AOB
Приложения:
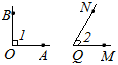
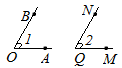
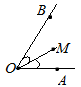
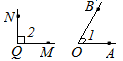
Автор ответа:
0
Большое спасибо!
Похожие вопросы
Предмет: Другие предметы,
автор: madrahimovamohlaroy
Предмет: Математика,
автор: ndhdndndj
Предмет: Математика,
автор: arunaalihan379
Предмет: Математика,
автор: limon23231