Предмет: Математика,
автор: lyalya1998
Решить систему по методу Крамера (если это возможно).
Приложения:
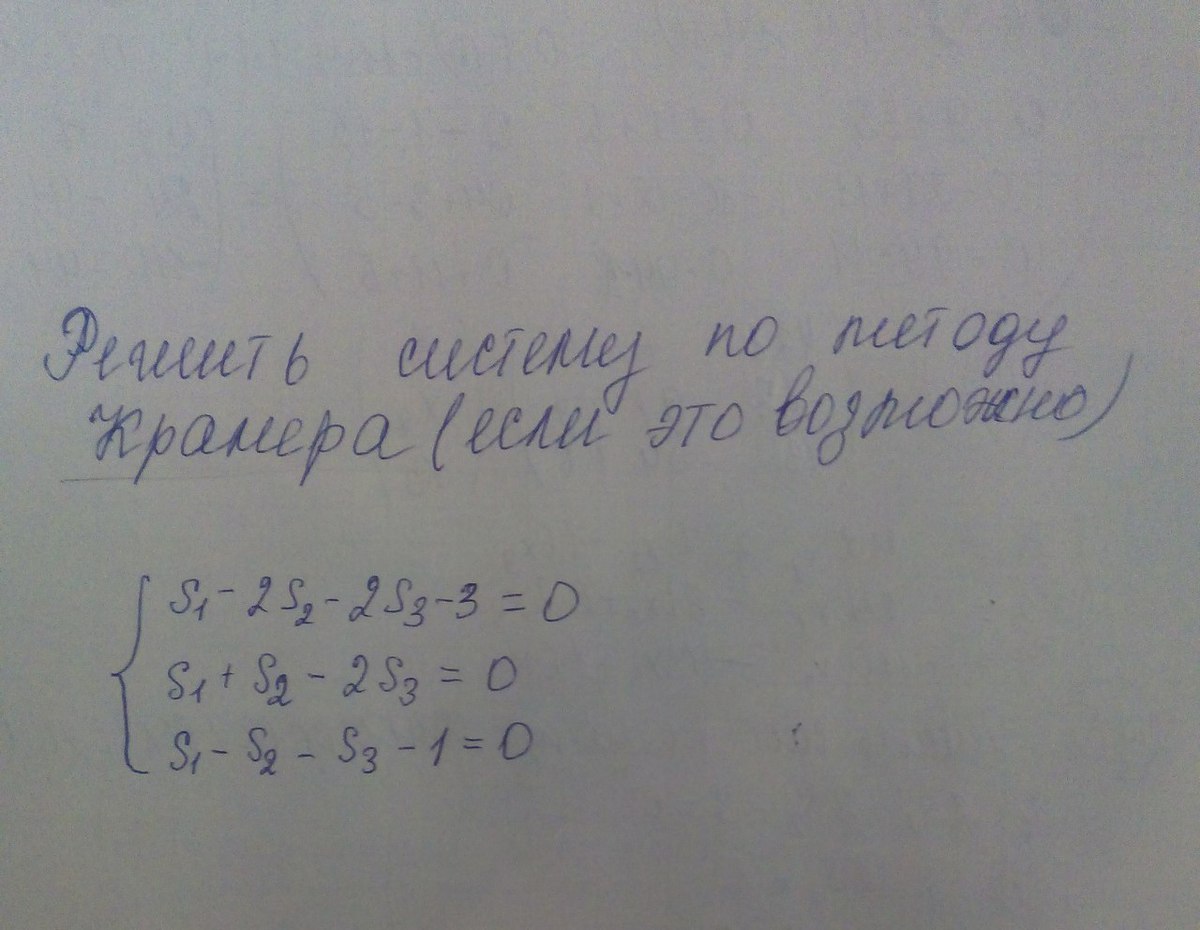
Ответы
Автор ответа:
0
Для вычисления определителя приводим матрицу к верхнетреугольному виду, используя элементарные преобразования над строками матрицы и свойства определителя матрицы.
поменяем 3-ую
строку и 4-ую
строку местами
0 -2 -2 -3 0 -2 -2 -3
∆ = 0 0 -2 0 = - 0 0 -2 0 = - 0*0*0*0=0
0 0 0 0 0 0 0 -1
0 0 0 -1 0 0 0 0
Ответ. Так как определитель матрицы равен нулю, то система не имеет решения.
поменяем 3-ую
строку и 4-ую
строку местами
0 -2 -2 -3 0 -2 -2 -3
∆ = 0 0 -2 0 = - 0 0 -2 0 = - 0*0*0*0=0
0 0 0 0 0 0 0 -1
0 0 0 -1 0 0 0 0
Ответ. Так как определитель матрицы равен нулю, то система не имеет решения.
Автор ответа:
0
сказано же методом крамера, а не гаусса
Автор ответа:
0
а как вам сбросить сюда решение я не могу...т.к уже один ответ написала
Автор ответа:
0
x2 = 0 x3 = 0 x4 = 0 x1 – свободная
Определитель основной матрицы равен нулю, значит система либо несовместна, либо имеет бесконечное множество решений. Ответить на этот вопрос поможет метод Гаусса.
Определитель основной матрицы равен нулю, значит система либо несовместна, либо имеет бесконечное множество решений. Ответить на этот вопрос поможет метод Гаусса.
Автор ответа:
0
просто будьте внимательнее при прочтении условия)
Похожие вопросы
Предмет: Литература,
автор: 0bulkasmakom0
Предмет: Математика,
автор: msatybaldina20
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: LizaMatis
Предмет: Алгебра,
автор: vvvvvddjjcdru