Предмет: Математика,
автор: pocik2015
Всем привет. Кто поможет с математикой?
Приложения:
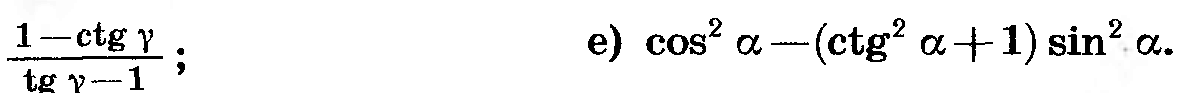
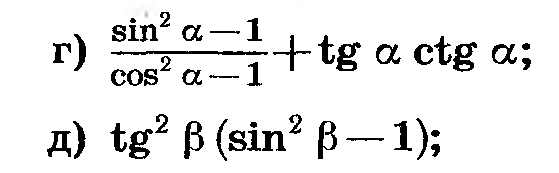

Ответы
Автор ответа:
0
Решение
1) (1 - ctgα)/(tgα - 1) = (tgα - 1)/ [tgα*(tgα - 1)= 1/tgα
2) cos²α - (ctgα + 1)*sin²α = cos²α - (1/sin²α)*sin²α = cos²α - 1
3) (sin²α - 1)/(cos²α - 1) + tgαctgα = (sin²α - 1 + cos²α - 1) /(cos²α) =
= 1/cos²α
4) tg²β*(sin²β - 1) = tg²β*(sin²β - sin²β - cos²β) = (sin²β/cos²β) * (- cos²β) =
= - sin²β
5) (1 - sinα)/cosα + tgα = (1 - sinα)/cosα + sinα/cosα =
(1 - sinα + sinα)/cosα =1/cosα
6) 1/(1 + cosα) + 1/(1 - cosα) = (1 - cosα + 1 - cosα) / (1 - cos²α) =
= 2/(1 - cos²α) = 2/(sin²α + cos²α - cos²α) = 2/sin²α
1) (1 - ctgα)/(tgα - 1) = (tgα - 1)/ [tgα*(tgα - 1)= 1/tgα
2) cos²α - (ctgα + 1)*sin²α = cos²α - (1/sin²α)*sin²α = cos²α - 1
3) (sin²α - 1)/(cos²α - 1) + tgαctgα = (sin²α - 1 + cos²α - 1) /(cos²α) =
= 1/cos²α
4) tg²β*(sin²β - 1) = tg²β*(sin²β - sin²β - cos²β) = (sin²β/cos²β) * (- cos²β) =
= - sin²β
5) (1 - sinα)/cosα + tgα = (1 - sinα)/cosα + sinα/cosα =
(1 - sinα + sinα)/cosα =1/cosα
6) 1/(1 + cosα) + 1/(1 - cosα) = (1 - cosα + 1 - cosα) / (1 - cos²α) =
= 2/(1 - cos²α) = 2/(sin²α + cos²α - cos²α) = 2/sin²α
Похожие вопросы
Предмет: Математика,
автор: zaykazZaya
Предмет: Литература,
автор: Аноним
Предмет: Химия,
автор: lokohik07
Предмет: Обществознание,
автор: maianh
Предмет: Алгебра,
автор: gromeanna