Помогите, пожалуйста, решить задачу:
ABCD- параллелограмм
AC=9, MC=MD=17, MA=16, MB перпендикулярен ABC
Найти: P(периметр)(ABCD)-?
Если можно, с объяснениями, где и от куда взялось.
Буду очень благодарна!)
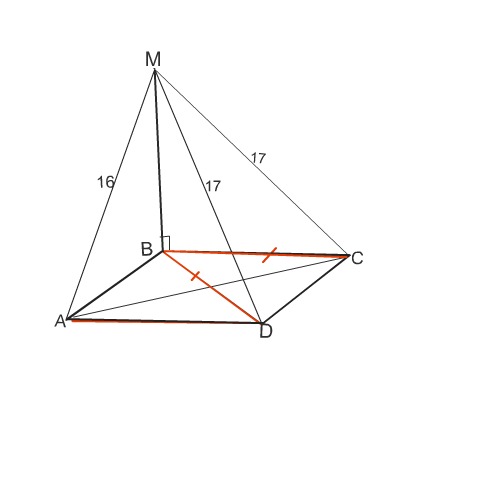
Рисунок: тетрайдер (вложение есть)

Ответы
ABCD- параллелограмм
AC=9, MC=MD=17, MA=16, MB перпендикулярен ABC
Найти: P(периметр)(ABCD)-?
---------------------------------------------------------------------------------
Смотрим рисунок во вложении
Решение:
АВ -проекция МА
ВС- проекция МС
ВD - проекция МD
МD=МС, значит, их проекции равны, т.к. эти наклонные проведены к плоскости треугольника из одной точки М.
ВС=ВD
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов двух смежных его сторон:
АС²+ВD=2(АВ² + ВС²)
ВС²=17²- МВ²
АВ²=16²- МВ²
АС²+ВD=2(16²- МВ² + 17²- МВ²)=512+ 578-4МВ²=1090-4МВ²
1090-4МВ²=АС²+ВD²
Но ВС=ВD, поэтому
1090-4МВ²=81+ВС²
Подставим значение ВС² из треугольника МВС
1090-4МВ²=81+17²-МВ²
1090-4МВ²=81+289-МВ²
1090-289-81=4МВ²-МВ²
3МВ²=1080
МВ²=240 ( нет нужды извлекать квадрат из 240, он не понадобится)
ВС²=17²-МВ²=289-240=49
ВС=√49=7
АВ²= МА²-МВ²=256-240=16
АВ=4
Периметр параллеллограмма
Р АВСD=2(АВ+ВС)=2(4+7)=22