Question

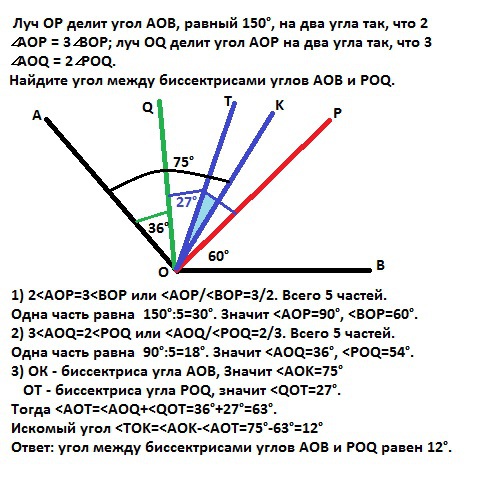
Луч OP делит угол AOB, равный 150°, на два угла так, что 2∠AOP = 3∠BOP; луч OQ делит угол AOP на два угла так, что 3∠AOQ = 2∠POQ. Найдите угол между биссектрисами углов AOB и POQ.

Answer 1

1) 2<AOP=3<BOP или <AOP/<BOP=3/2. Всего 5 частей.
Одна часть равна  150°:5=30°. Значит <AOР=90°, <BOP=60°.
2) 3<AOQ=2<POQ или <AOQ/<POQ=2/3. Всего 5 частей.
Одна часть равна  90°:5=18°. Значит <AOQ=36°, <POQ=54°.
3) ОК - биссектриса угла АОВ, Значит <AOK=75°
   ОТ - биссектриса угла POQ, значит <QOT=27°.
Тогда <AOT=<AOQ+<QOT=36°+27°=63°.
Искомый угол <TOK=<AOK-<AOT=75°-63°=12°
Ответ: угол между биссектрисами углов АОВ и РОQ равен 12°.