Question

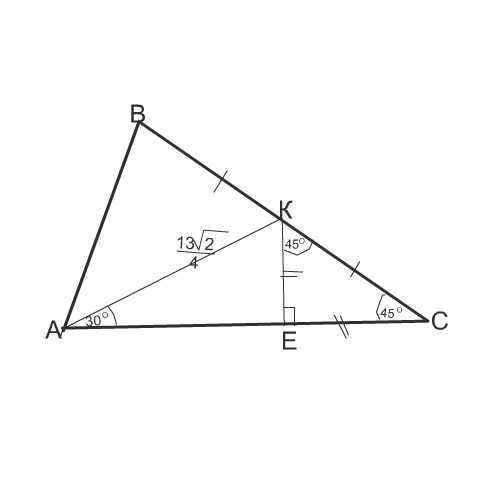
В Треугольнике АВС проведена медиана АК равная $13sqrt{2}/4$  и составляющая со стороной АС угол 30. Найти ВС если угол ВСА 45

Answer 1

сделаем постороение по условию

медиана АК  составляющая со стороной АС угол CAK=30.

 АК = 

по теореме синусов

 

АК / sin BCA = CK / sin CAK

CK = АК *sin CAK / sin BCA 

BC = 2*CK = 2*АК*sinCAK /sinBCA=2*13√2/4*sin30 /sin45 = 6.5 

 

ОТВЕТ    ВС=6.5

 

Answer 2

Эта задача имеет и другое решение, без применения теоремы синусов.

Из точки К опустим к АС перпендикуляр КЕ. Получим прямоугольный треугольник АКЕ.

По свойству катета, противолежащего углу 30°,

он равен половине медианы АК и КЕ равен (13√2):8
Так как угол С=45°, то Δ КЕС равнобедренный прямоугольный и

ЕС=КЕ=(13√2):8
Найдя КС и умножив на 2, найдем ВС
КС можно вычислить по теореме Пифагора, а можно по формуле диагонали квадрата,т.к. треугольник КЕС - половина квадрата с диагональю КС.
d=а√2
КС=КЕ√2=√2(13√2):8=26:8
ВС=2(26:8)=52:8=6,5