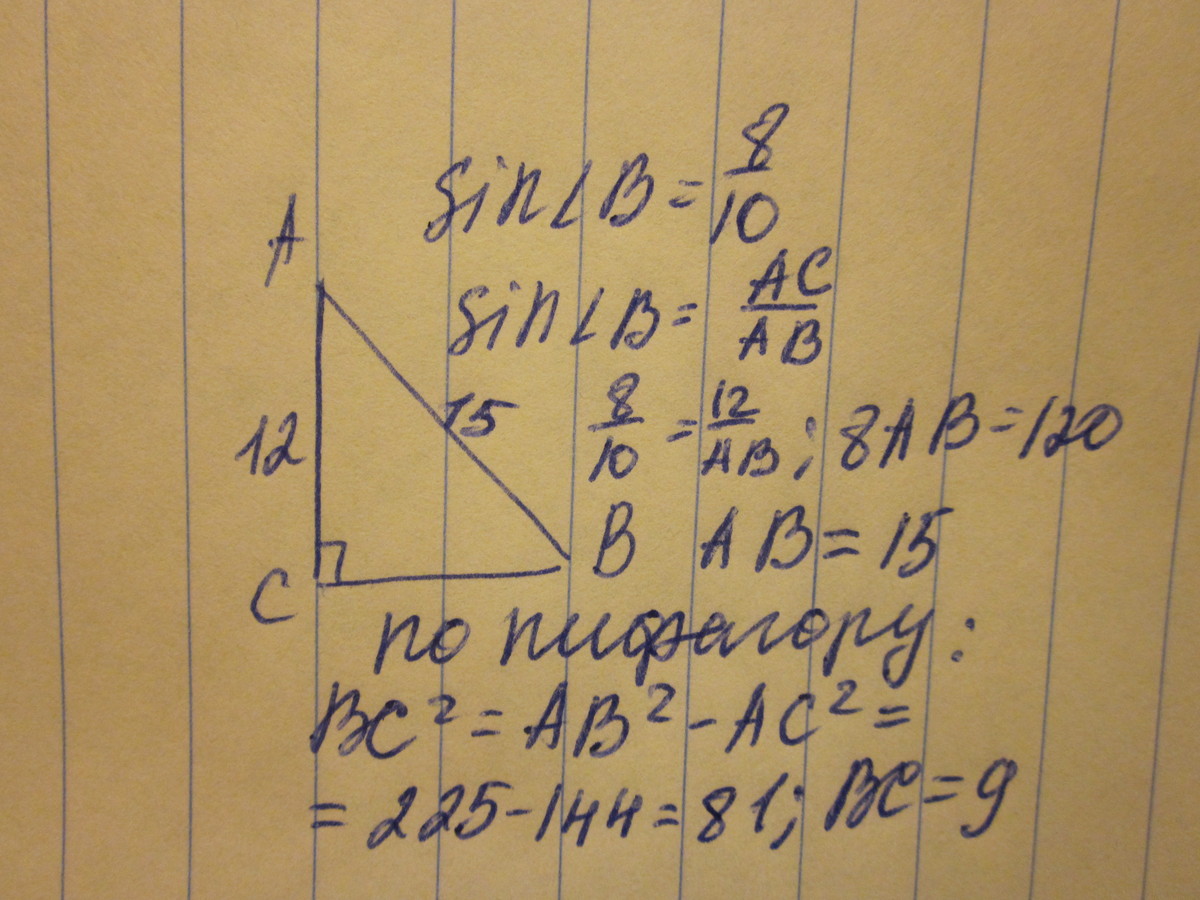1.В треугольнике АВС угол А прямой, АС=12см, sin угла АВС=0,8. Найдите ВС.
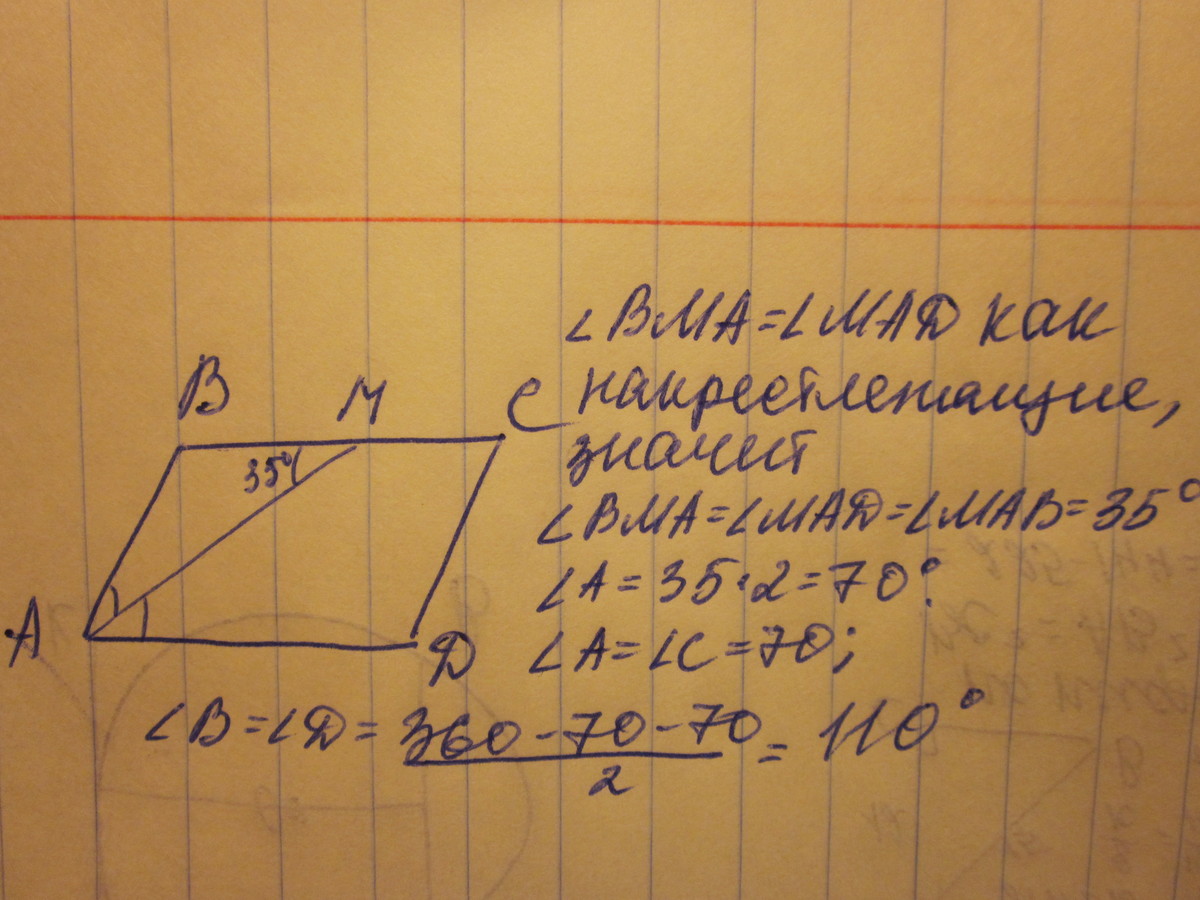
2.Найдите величины углов параллелограмма АВСD, если биссектриса угла А образует со стороной ВС угол, равный 35 градусам.
Ответы
1)
СВ- гипотенуза, АС и ВА - катеты
sin ∠АВС=0,8
АВ:СВ=0,8
Пусть коэффициент этого отношения х.
Тогда АВ=8х, ВС=10х
По теореме Пифагора
СВ²-ВА²=АС²
100х²-64х²=144
36х²=144
х²=4
х=2
ВС=2*10=20
----------------------------------
2
)По свойству углов при пересечении параллельных прямых секущей
биссектриса АК угла А образует со сторонами параллелограмма равнобедренный треугольник АВК, так как углы, отмеченны на рисунке как
∠1 и ∠2 - накрестлежащие.
а ∠1 является половиной ∠А
Отсюда ∠ А=2*35=70°, а так как сумма углов при одной стороне параллелограмма равна 180°, то
∠В=180°-70°=110°
Ответ:
∠А=∠С=70°
∠В=∠D=110°
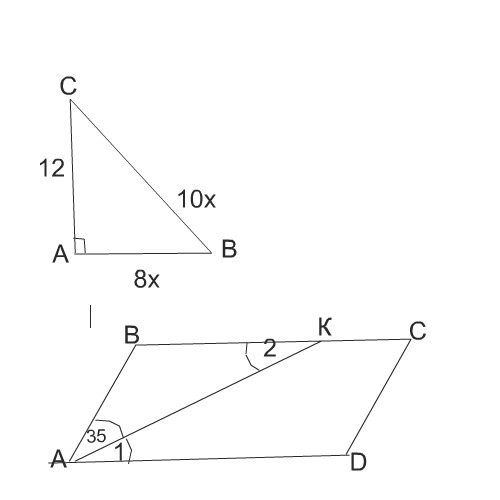
всё решение на фотографиях