Предмет: Математика,
автор: 909922990
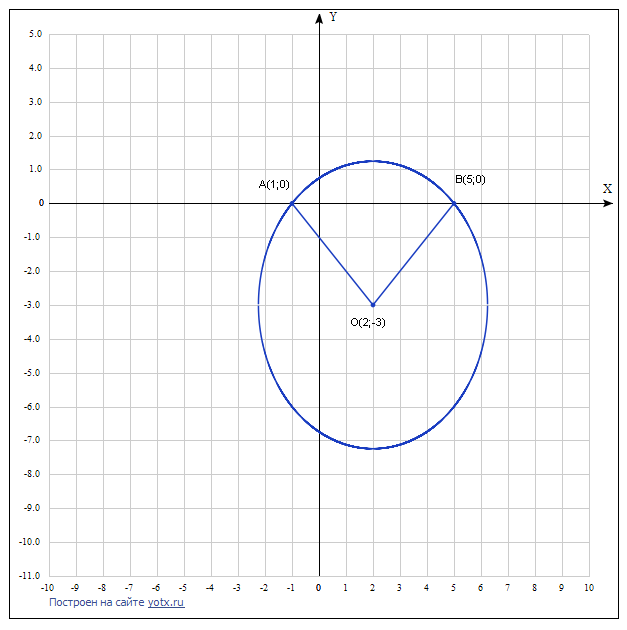
Найти угол между радиусами окружности х2 + у2 - 4х + 6у - 5= 0, проведенными в точки пересечения ее с осью Ох
Ответы
Автор ответа:
0
Приложения:
Автор ответа:
0
как нашли точки А и В
Похожие вопросы
Предмет: Обществознание,
автор: mariastefanisina
Предмет: Математика,
автор: natalagajdenko123
Предмет: Русский язык,
автор: ostapenkoalexa12
Предмет: Литература,
автор: tanychka1985