Предмет: Алгебра,
автор: airdal
Задано выражение:
Докажите, что значение данного выражения положительно при всех допустимых значениях переменной.
Приложения:
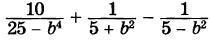
Ответы
Автор ответа:
0
Любое число в квадрате положительно, поэтому это выражение будет принимать только положительные значения.
Похожие вопросы
Предмет: Астрономия,
автор: vivinet
Предмет: История,
автор: Sanko22229
Предмет: Химия,
автор: mavilesatterova
Предмет: Обществознание,
автор: Всезнайка264
Предмет: Математика,
автор: stasyan43rus