Предмет: Математика,
автор: martiemiliya
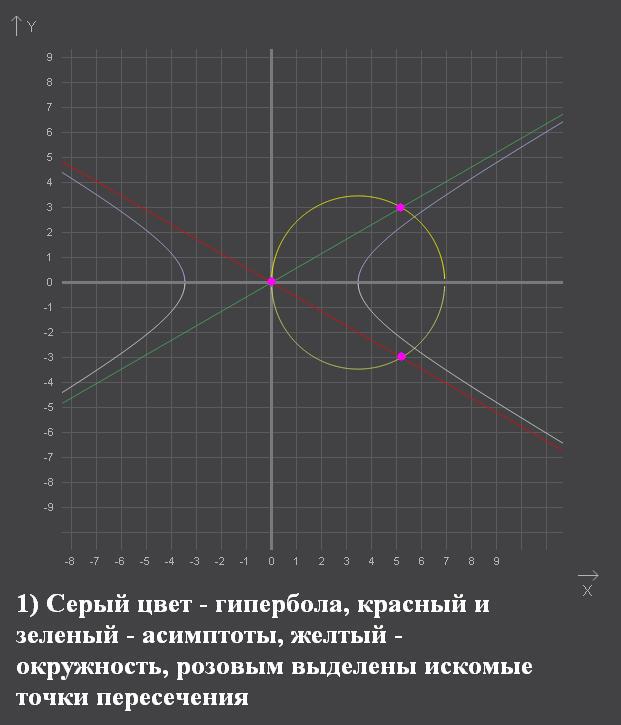
№1. Найти точки пересечения асимптот гиперболы х²-3у²=12 с окружностью,имеющей центр в правом фокусе гиперболы и проходящей через начало координат.
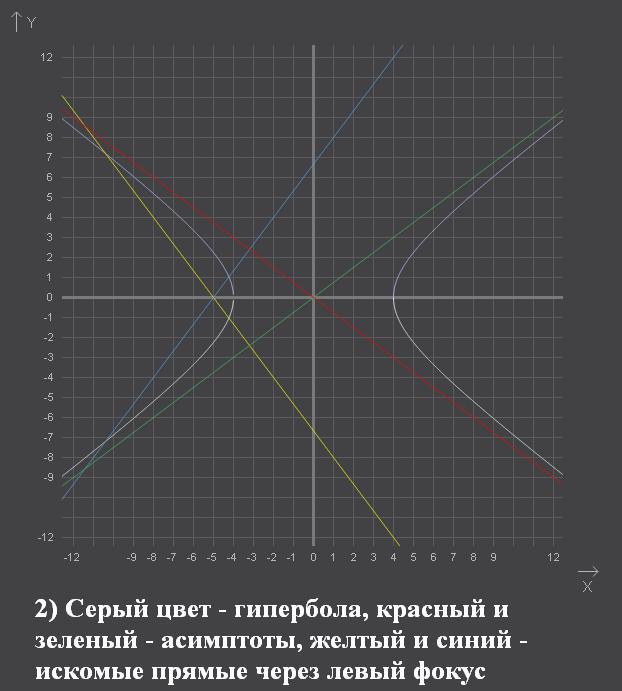
№2. Гипербола проходит через точку М(6; 3√5/2),симметрична относительно осей координат и имеет вещественную полуось а=4. Написать уравнения перпендикуляров ,опущенных из левого фокуса гиперболы на ее асимптоты.
С подробным решением и объяснением ,пожалуйста! :)
Ответы
Автор ответа:
0
1.
Уравнение гиперболы имеет стандартный вид: , где а и b - полуоси гиперболы
, где а и b - полуоси гиперболы

Значит, у гиперболы
Правый фокус гиперболы имеет вид F(c; 0), где
Находим с:

Так как окружность проходит через начало координат, то ее радиус равен абсциссе правого фокуса, то есть
Общий вид уравнения окружности: , где
, где  - центр окружности, R - ее радиус
- центр окружности, R - ее радиус
Уравнение окружности:
Асимптоты гиперболы имеют вид:
Тогда, асимптоты гиперболы
Подставляем в уравнение окружности выражение для у:

Тогда у для соответствующих х равны:

Ответ: ;
;  ;
; 
2.
Так как известна одна полуось и точка, принадлежащая гиперболе, о можно найти вторую полуось:

Тогда уравнения асимптот принимают вид:
Угловой коэффициент перпендикулярной прямой является обратным и противоположным числом к угловому коэффициенту исходной прямой:
Тогда, для прямой таким коэффициентом является число
таким коэффициентом является число  , а для прямой
, а для прямой  - число
- число 
Левый фокус гиперболы имеет вид F(-c; 0), где
 , следовательно через точку (-5; 0) нужно провести искомые прямые
, следовательно через точку (-5; 0) нужно провести искомые прямые
Уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом k имеет вид:
с заданным угловым коэффициентом k имеет вид: 
Тогда:

Или по отдельности:

Уравнение гиперболы имеет стандартный вид:
Значит, у гиперболы
Правый фокус гиперболы имеет вид F(c; 0), где
Находим с:
Так как окружность проходит через начало координат, то ее радиус равен абсциссе правого фокуса, то есть
Общий вид уравнения окружности:
Уравнение окружности:
Асимптоты гиперболы имеют вид:
Тогда, асимптоты гиперболы
Подставляем в уравнение окружности выражение для у:
Тогда у для соответствующих х равны:
Ответ:
2.
Так как известна одна полуось и точка, принадлежащая гиперболе, о можно найти вторую полуось:
Тогда уравнения асимптот принимают вид:
Угловой коэффициент перпендикулярной прямой является обратным и противоположным числом к угловому коэффициенту исходной прямой:
Тогда, для прямой
Левый фокус гиперболы имеет вид F(-c; 0), где
Уравнение прямой, проходящей через заданную точку
Тогда:
Или по отдельности:
Приложения:
Автор ответа:
0
Идеальное решение! ВЫ молодец!!!!!
Похожие вопросы
Предмет: Другие предметы,
автор: artur250805
Предмет: Математика,
автор: darinaakhmedova13
Предмет: Русский язык,
автор: almirasagumbaeva
Предмет: Литература,
автор: Мария1314