Предмет: Алгебра,
автор: AnyGool
Помогите пожалуйста решить через определительΔ=
(матрица)
см.вложение
Приложения:
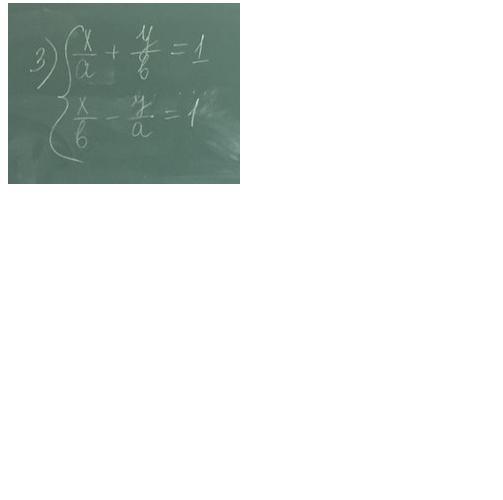
Ответы
Автор ответа:
0
решение во вложении------------------------------------
Приложения:
Автор ответа:
0
1 способ - метод Крамера


Составляем определитель:

Составляем определитель, заменив в предыдущем определителе коэффициенты при х на соответствующие свободные члены:

По формуле находим х:

Составляем определитель, заменив коэффициенты при у в первом определителе на соответствующие свободные члены:

Находим у:

Ответ:
2 способ - метод Гаусса

Составляем расширенную матрицу:

Первую строку домножаем на а, вторую - домножаем на b:

От элементов первой строки отнимем элементы второй:

Значит:

Из второго уравнения выражаем х:

Заменяем у найденным значением:

Получаем ответ, совпадающий с ответом, получившимся при решении первым способом.
Ответ:
Составляем определитель:
Составляем определитель, заменив в предыдущем определителе коэффициенты при х на соответствующие свободные члены:
По формуле находим х:
Составляем определитель, заменив коэффициенты при у в первом определителе на соответствующие свободные члены:
Находим у:
Ответ:
2 способ - метод Гаусса
Составляем расширенную матрицу:
Первую строку домножаем на а, вторую - домножаем на b:
От элементов первой строки отнимем элементы второй:
Значит:
Из второго уравнения выражаем х:
Заменяем у найденным значением:
Получаем ответ, совпадающий с ответом, получившимся при решении первым способом.
Ответ:
Приложения:
Автор ответа:
0
Спасиииибооо огромное..Слов нет!!!!!)))))))))спасиибоо_)
Похожие вопросы
Предмет: Русский язык,
автор: defund
Предмет: Английский язык,
автор: koloskovamariana
Предмет: Русский язык,
автор: kad007096
Предмет: Математика,
автор: ЛЛЛЛиииииииннннннааа