Question

Буду очень благодарна за помощь! Плиз!  :)

Answer 1

Для решения задачи нужно найти радиус r искомого сечения. 

Его площадь равна 64 см²

Формула площади круга 

   S=πr²

r²=S:π=64π:π=64 см²

r=√ 64=8 см

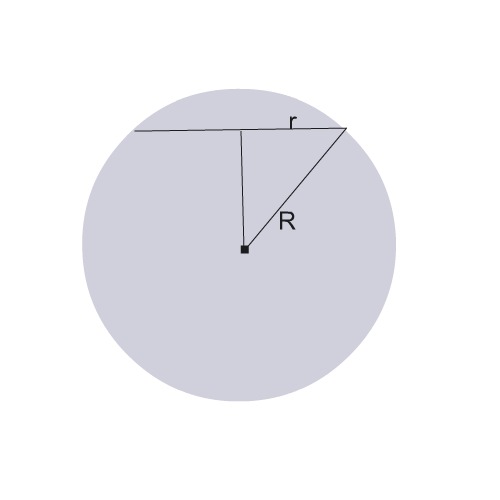
Сделаем рисунок. 

Проведем хорду. означающую диаметр сечения. 

Диаметр сечения отстоит от центра шара на х см

Соединим один из концов этого диаметра и его середину с центром шара.

Получим прямоугольный треугольник с катетом, равным радиусу r сечения и гипотренузой, равной радиусу R шара.Он равен половине его диаметра =34:2=17 см

Отрезок,. соединяющий два центра, и будет искомым расстоянием х и вторым катетом треугольника. 

По теореме Пифагора 

х²=R²- r²

Подставим в уравнение значения радиусов

х²=17²-8²=225 см²

х=√225=15 см

Ответ: 15 см нужное расстояние.