Предмет: Геометрия,
автор: Аноним
радиус основания конуса равен 4 см . Осевым сечением служит прямоугольный треугольник
.Найдите его площадь
Ответы
Автор ответа:
0
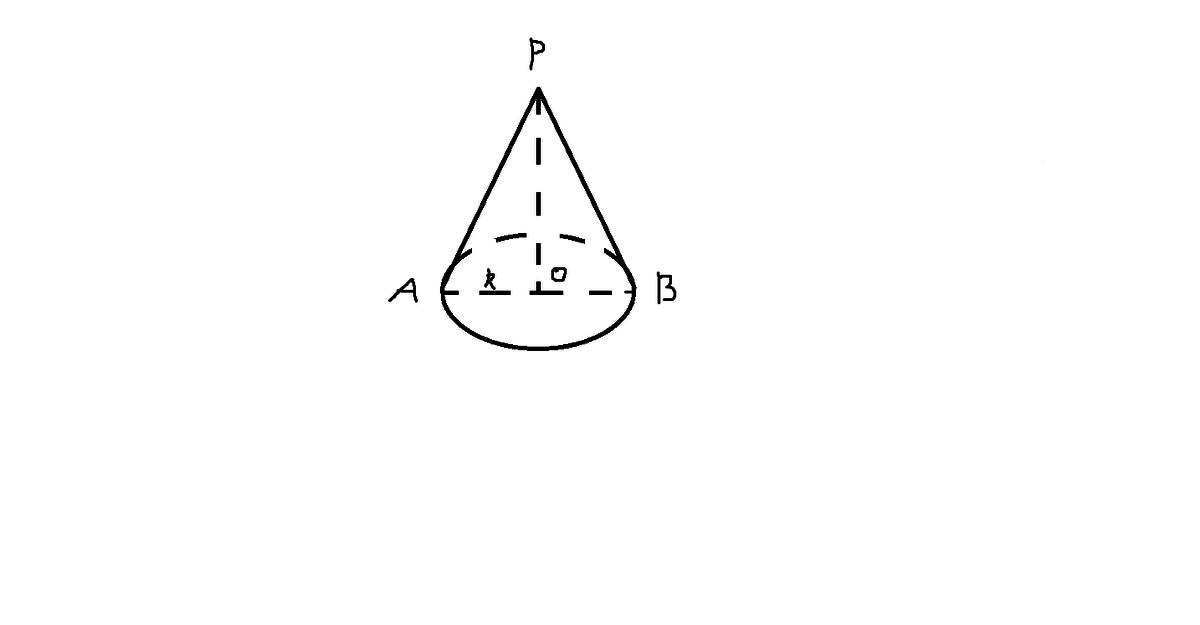
Пусть ∠APB=90°.




По теореме Пифагора.




По теореме Пифагора.
Приложения:
Автор ответа:
0
Спасибо Вам огромное!!!!
Автор ответа:
0
Обновите страницу, изменил ответ.
Автор ответа:
0
сейчас)
Автор ответа:
0
Работать будем с Теоремой Пифагора,
∵∴точка О-центр окружности , R-радиус
AO=OB=4см
Найдем площадь треугольника
SΔabd=1/2ad*db⇒1/2ad²
2AD²=AB²
Вот и теорема Пифагора нужна ↓
AD=8(2R=2*4)
2AD²=64
AD²=32
Подставляем в ранею площадь
Sadb=32/2=16см²
ОТВЕТ:16см²
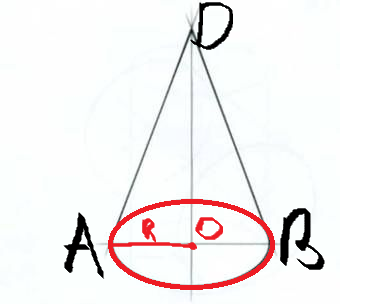
рисунок прилагается
∵∴точка О-центр окружности , R-радиус
AO=OB=4см
Найдем площадь треугольника
SΔabd=1/2ad*db⇒1/2ad²
2AD²=AB²
Вот и теорема Пифагора нужна ↓
AD=8(2R=2*4)
2AD²=64
AD²=32
Подставляем в ранею площадь
Sadb=32/2=16см²
ОТВЕТ:16см²
рисунок прилагается
Приложения:
Похожие вопросы
Предмет: Астрономия,
автор: GOsha200877
Предмет: Физика,
автор: ArstanbekovaAelina
Предмет: Математика,
автор: StepanovaUwU12
Предмет: Литература,
автор: 55pantera55
Предмет: Биология,
автор: ssmirnova219