Предмет: Алгебра,
автор: Аноним
докажите что уравнение правильно
Приложения:
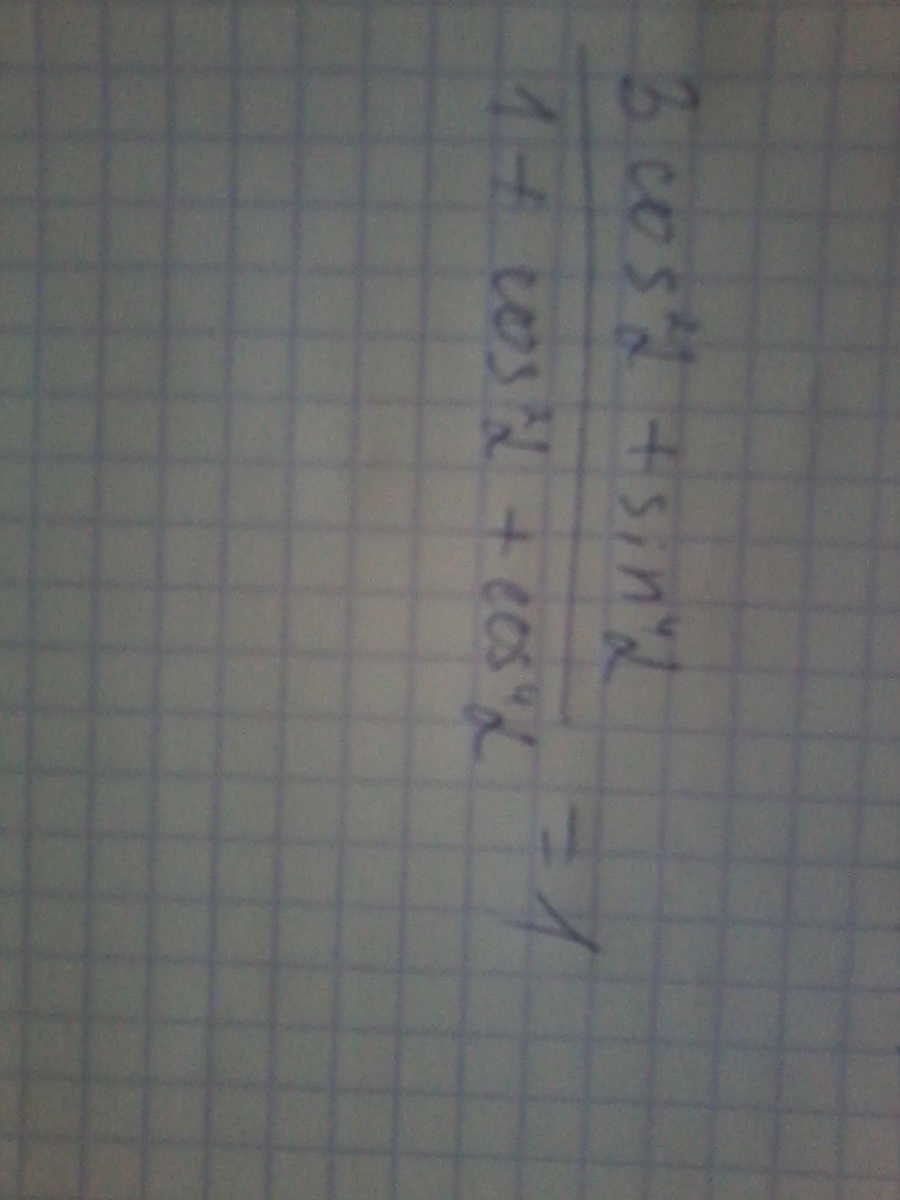
Ответы
Автор ответа:
0
Упростим левую часть:
Использовались формулы:
1) Основное тригонометрическое тождество и следствие из него:
2) Формула сокращенного умножения - квадрат разности:
Похожие вопросы
Предмет: Математика,
автор: KarinaBaibysinova
Предмет: Математика,
автор: Аноним
Предмет: Геометрия,
автор: apro0872
Предмет: Химия,
автор: AnnyG
Предмет: География,
автор: КейтГрафова