Предмет: Алгебра,
автор: 49Юлька59
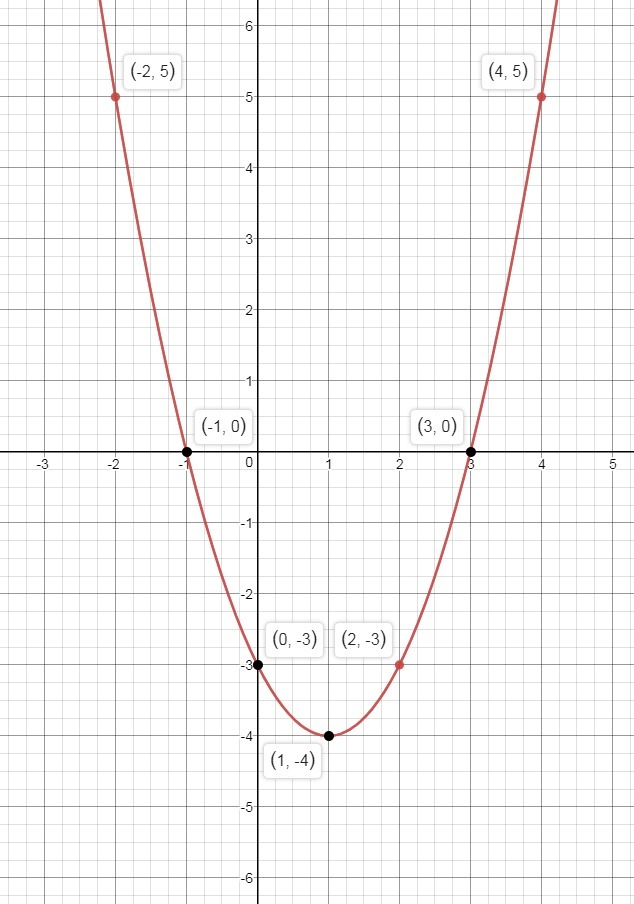
Подскажите как решить.Постройте график функции y=x в квадрате минус 2х минус 3.
С помощью графика найдите:
а)промежутки возрастания и убывания функции
б)наименьшее и наибольшее значения функции
в)при каких значениях х и у меньше нуля
Ответы
Автор ответа:
0
Постройте график функции

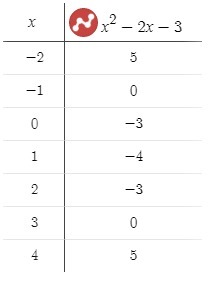
Табличные данные для построения графика представлены ниже
a) Промежутки возрастания и убывания функции
Заданный график функции является параболой, т.к. а=1 >0 то ветви направлены вверх, значит слева от вершины график убывает, а справа от вершины возрастает.
Найдем вершину параболы

Тогда промежуток убывания функции
![(-
infty ; 1] (-
infty ; 1]](https://tex.z-dn.net/?f=%28-%0Ainfty++%3B++1%5D)
возрастания

б) Так как ветви параболы направлены вверх, то наибольшего значения - нет, наименьшее значение функции будет в вершине, при х =1

в) Найдем на графике, при каких значения У функция меньше нуля при

Для нахождения значений Х , необходимо решить
Решим квадратное уравнение

Вычислим дискриминант

Корни квадратного уравнения


тогда
Или такое же решение можно взять с графика. Здесь необходимо найти точки пересечения графика с осью ОХ и взять те значения Х при которых график функции будет находится строго ниже оси ОХ. На рисунке видно что это точки х=-1 и х=3, т.е.
Табличные данные для построения графика представлены ниже
a) Промежутки возрастания и убывания функции
Заданный график функции является параболой, т.к. а=1 >0 то ветви направлены вверх, значит слева от вершины график убывает, а справа от вершины возрастает.
Найдем вершину параболы
Тогда промежуток убывания функции
возрастания
б) Так как ветви параболы направлены вверх, то наибольшего значения - нет, наименьшее значение функции будет в вершине, при х =1
в) Найдем на графике, при каких значения У функция меньше нуля при
Для нахождения значений Х , необходимо решить
Решим квадратное уравнение
Вычислим дискриминант
Корни квадратного уравнения
тогда
Или такое же решение можно взять с графика. Здесь необходимо найти точки пересечения графика с осью ОХ и взять те значения Х при которых график функции будет находится строго ниже оси ОХ. На рисунке видно что это точки х=-1 и х=3, т.е.
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: gofmanartur36
Предмет: Биология,
автор: darinapopova50
Предмет: Английский язык,
автор: alinasagitova08
Предмет: Математика,
автор: bashnat65