Предмет: Геометрия,
автор: Alinka0115
Диаметр СД и хорда АВ взаимно перпендикулярны и пересекаются в точке Е, СЕ=4 АВ+СЕ=СД найти радиус окружности.
Ответы
Автор ответа:
0
СД - диаметр.
АВ - хорда.
АВ+СЕ=СД
ЕД+СЕ=СД⇒
АВ=ЕД
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
АЕ=ВЕ
Произведения длин отрезков, на которые разбита каждая из хорд при их пересечении, равны.
Диаметр - наибольшая хорда окружности.
Пусть половина АВ=х
Тогда АВ=2х, ⇒ ЕД=2х
х*х=4*2х
х=8
АВ=ЕД=8·2=16
СД=СЕ+ЕД=4+16=20
r=СД:2=20:2=10
АВ - хорда.
АВ+СЕ=СД
ЕД+СЕ=СД⇒
АВ=ЕД
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
АЕ=ВЕ
Произведения длин отрезков, на которые разбита каждая из хорд при их пересечении, равны.
Диаметр - наибольшая хорда окружности.
Пусть половина АВ=х
Тогда АВ=2х, ⇒ ЕД=2х
х*х=4*2х
х=8
АВ=ЕД=8·2=16
СД=СЕ+ЕД=4+16=20
r=СД:2=20:2=10
Приложения:
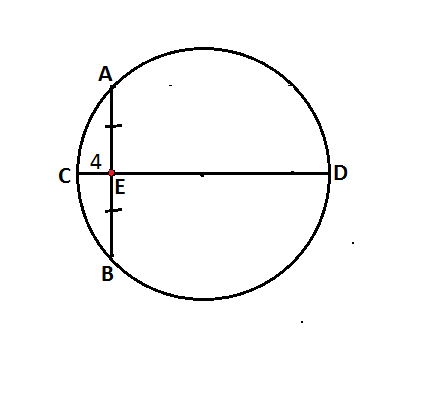
Похожие вопросы
Предмет: Русский язык,
автор: jainagul2205
Предмет: География,
автор: dima9213
Предмет: Биология,
автор: CharlieFletcher
Предмет: Математика,
автор: Ceni2005
Предмет: Информатика,
автор: Kettyyy