Question

Планиметрия 10 класс, помогите пожалуйста
И если можно, то все по полочкам расскажите с:
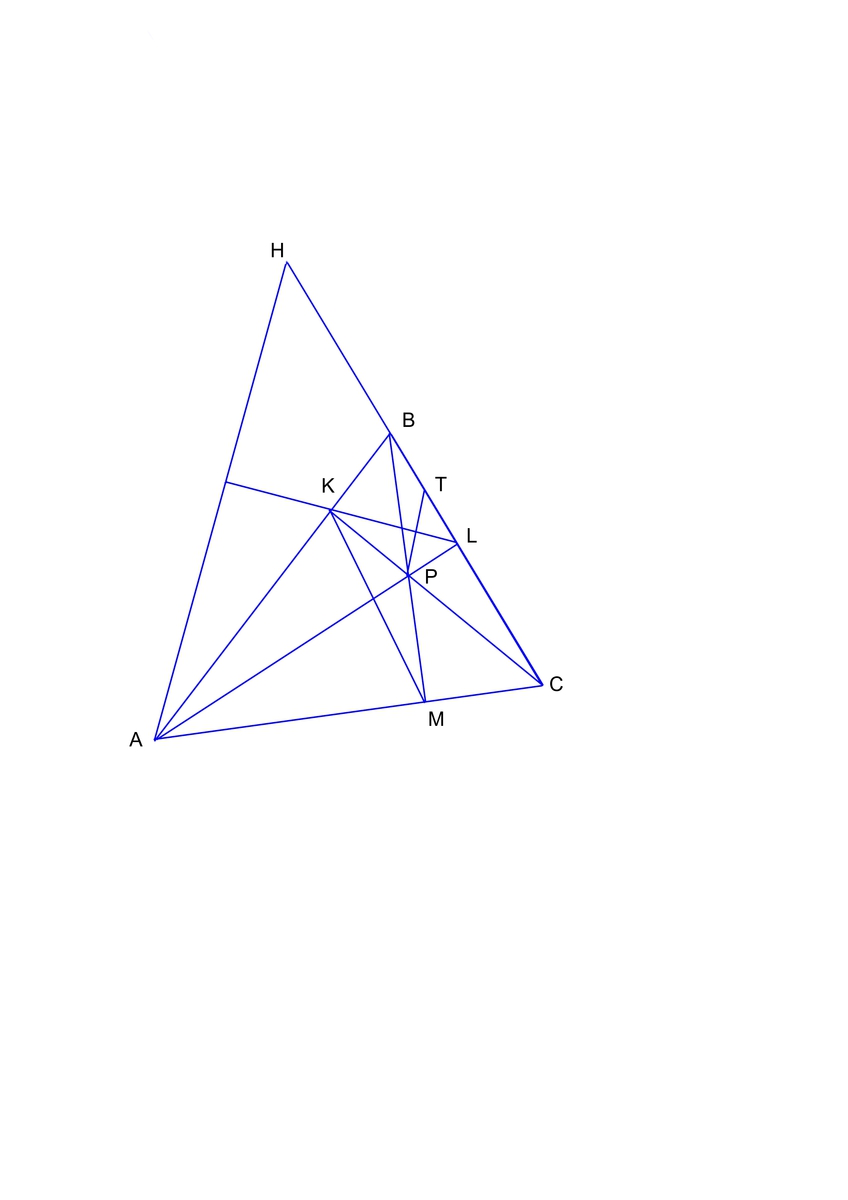
2 фото мой рисунок

Answer 1

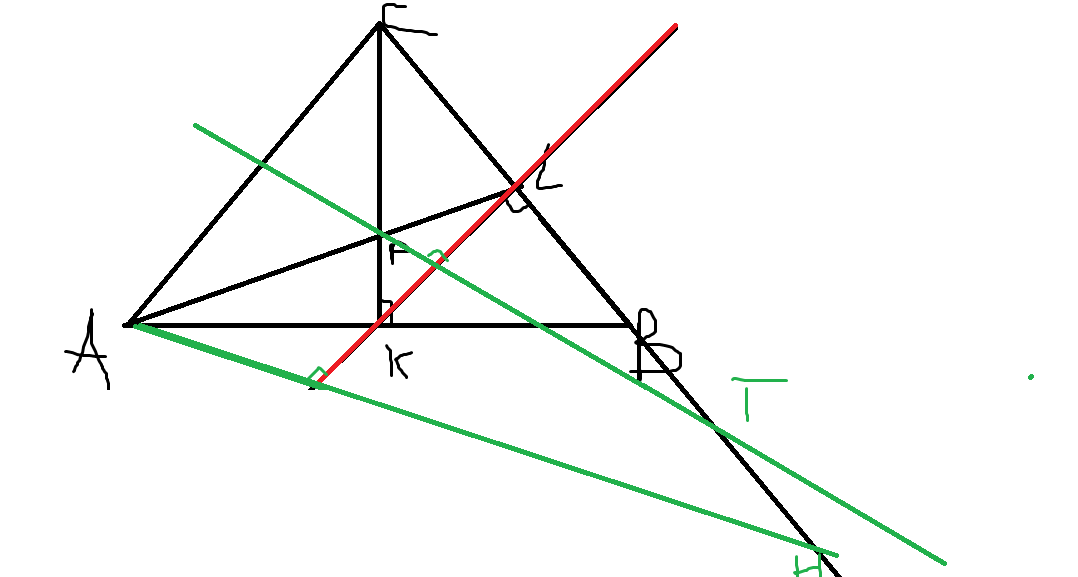
Треугольник BKL имет стороны  BL = AB*cos(B) и BK = BC*cos(B) и угол B, общий с треугольником ABC. Поэтому этот треугольник подобен треугольнику ABC с коэффициентом подобия cos(B);
отсюда следует, что KL = AC*cos(B); и ∠KLB = ∠BAC
Точно также доказывается подобие треугольников ABC и AKM (BM - третья высота треугольника ABC) и равенство KM = BC*cos(A).
Поскольку ∠KLB = ∠BAC, то ∠AHL = 90° - ∠KLB = 90° - ∠BAC;
поэтому ∠HAL = ∠TPL = ∠BAC (или просто угол A треугольника ABC);
Легко видеть что HT = HL - TL = AL*tg(A) - PL*tg(A) = AP*tg(A);
HT = AP*sin(A)/cos(A);
Окружность, построенная на AP, как на диаметре, пройдет через точки K и M, то есть будет описанной для треугольника AKM; то есть
AP*sin(A) = KM; (это теорема синусов :)), а (как показано в начале) KM = BC*cos(A);
откуда HT = BC = 6;

Answer 2

н-да... видимо еще через две недели последует новый вопрос...

Answer 3

А что, если сообразит - сильно продвинется, а нет - какой смысл мне повторять решение еще раз?

Answer 4

согласна...

Answer 5

Я ведь в первом абзаце объясняю про подобие BKL и ABC. Почему же, если это понятно - то возникают вопросы про треугольник AKM? или CML? там какие то другие углы, не плоские? или стороны не прямые? :) Однако - спрашивают... эх :(((

Answer 6

подобие--тяжелая тема... не все понимают... значит, и это было не понятно...