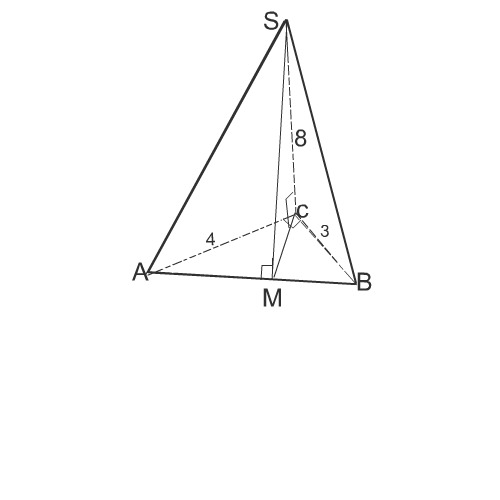
В основании треугольной пирамиды лежит прямоугольный треугольник с прямым углом С и катетами 3 и 4. Высота пирамиды SC равна 8. Плоскость, проходящая через ребро SC, дает в пересечении с пирамидой треугольник SDC наименьшей площади. Найдите площадь этого сечения.
Ответы
На этой странице у меня цифры 3 в значении катета по какой-то причине не видно в условии задачи, но скопировала ее часть и видно это: "треугольник с прямым углом С и катетами 3 и 4"
-------------------------------В рисунке и задаче я вместо SDC употребила SМC, но это на решение не влияет.
Решение:
Сечение, дающее треугольник SМC наименьшей площади - это сечение, в основании которого лежит высота треугольника АВС, т.к. остальные отрезки из С к АВ длиннее перпендикуляра как наклонные.
Площадь этого сечения ( прямоугольного треугольника SCМ) найдем половиной произведения катетов:
S сечения= СМ·SМ:2
СМ - высота треугольника с катетами 3 и 4.
Этот треугольник АВС - египетский, и без вычислений можно вспомнить, что его
гипотенуза равна 5. Применив теорему Пифагора получим ту же самую величину.
Найдем высоту этого треугольника из двух форул:
СМ²=АС²-АМ²
СМ²=СВ²- МВ²
Приравняем эти значения высоты:
АС²-АМ²=СВ²- МВ²
Пусть АМ=х, тогда МВ=5-х
16-х²=9 - (5-х)²
16-х²=9 - 25 +10х-х²
16 =9 - 25 +10х
10х=32
х=3,2
5-х=1,8
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
h²=АМ·МВ
h =√3,2·1,8=2,4
СМ=2,4
S сечения= СМ·SМ:2
S сечения= 2,4·8:2=9,6 см²