Предмет: Алгебра,
автор: Аноним
Помогите решить интеграллы. Нужно полное решение!
Приложения:

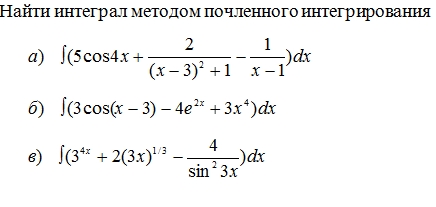
Ответы
Автор ответа:
0
Первые три только, а то поздно уже :)
а)
б)
,
б)
,
б)
,
,
,
Автор ответа:
0
А я, пожалуй, остальные добью.
г)
д)
Почленное интегрирование
а)
б)
в)
Похожие вопросы
Предмет: Українська мова,
автор: evamatiiva
Предмет: Литература,
автор: semejsemej46
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Алгебра,
автор: Dobrak
Предмет: Математика,
автор: diima03