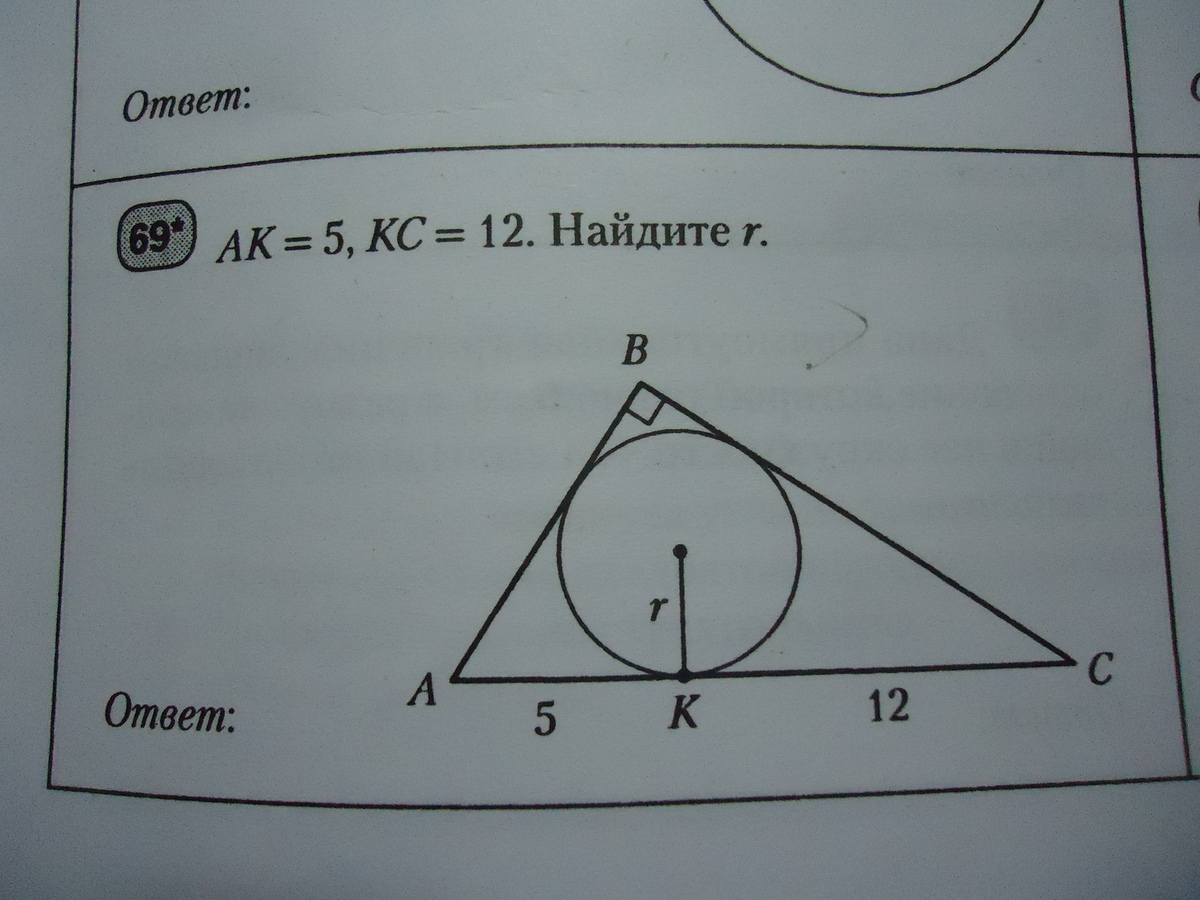
AK=5; KC=12. Найдите r прямоугольного треугольника с вписанной окружностью
Ответы
Ну, "в лоб" решать надо так - из центра окружности проводятся радиусы в точки касания, то есть перпендикуляры к катетам, и там получается квадрат (его образуют эти радиусы и касательные из вершины прямого угла), то есть катеты равны r + 5 и r + 12.
Дальше все по Пифагору :)
(r + 5)^2 + (r + 12)^2 = (5 + 12)^2;
r^2 + 17r - 60 = 0;
r = 3; (отрицательный корень не подходит).
А вот более умное решение находится гораздо проще :).
Поскольку гипотенуза равна 5 + 12 = 17, то сразу вспоминается :) что есть такой прямоугольный треугольник со сторонами 8, 15, 17.
(Это называется Пифагорова тройка, 8^2 + 15^2 = 17^2)
Проверяем, чему равен r... r = (8 + 15 - 17)/2 = 3; и отрезки касательных как раз и получаются 3, 5 и 12.
Как можно убедиться, подбором решение получается гораздо быстрее.