Предмет: Алгебра,
автор: wolfsdiary
Найдите нули функции,промежутки законопостоянства, промежутки возрастания и убывания функции:
1)y=I x-3 I - 1
2) y=x²-4
Ответы
Автор ответа:
0
2) Найдите нули функции,промежутки законопостоянства, промежутки возрастания и убывания функции 
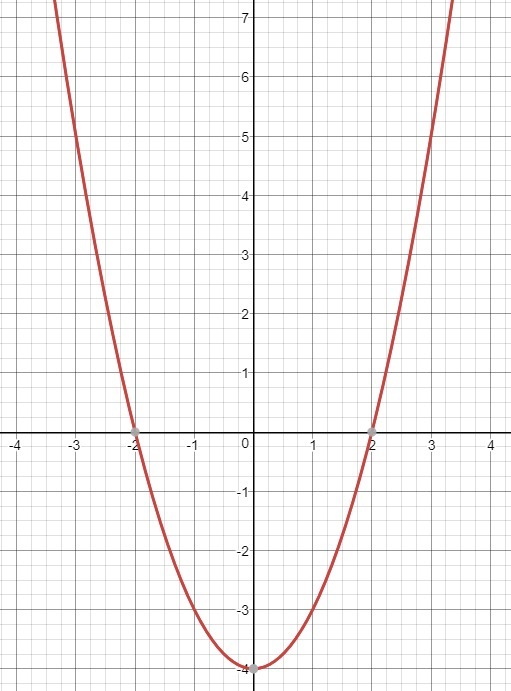
a) Нули функции

т.е. число 2 и -2 -- ноли этой функции
б) Промежутки законопостоянства, для этого найдем когда

и

Нули функции мы уже находили , кроме того функция представляет собой параболу.
, кроме того функция представляет собой параболу.
Т.к. а=1 > 0 , то ветви направлены вверх, значит:
на промежутке - функция принимает положительные значения; в промежутке
- функция принимает положительные значения; в промежутке  отрицательные и в промежутке
отрицательные и в промежутке  — положительные.
— положительные.
в) Промежутки возрастания и убывания функции.
Найдем вершину параболы

Тогда парабола убывает и возрастает
и возрастает 
Для наглядности смотри рисунок, ниже
1) Найдите нули функции,промежутки законопостоянства, промежутки возрастания и убывания функции
a) Нули функции

Раскроем модуль

и

т.е. число 2 и 4 -- ноли этой функции
б) Промежутки законопостоянства, для этого найдем

Тогда

Значит, в промежутке - функция принимает положительные значения, в промежутке
- функция принимает положительные значения, в промежутке  — отрицательные и в промежутке
— отрицательные и в промежутке  — положительные
— положительные
в) Промежутки возрастания и убывания функции.
Функция убывает в промежутках (−∞; 3) и возрастает в промежутке (3;+∞). Смотри рисунок ниже
a) Нули функции
т.е. число 2 и -2 -- ноли этой функции
б) Промежутки законопостоянства, для этого найдем когда
и
Нули функции мы уже находили
Т.к. а=1 > 0 , то ветви направлены вверх, значит:
на промежутке
в) Промежутки возрастания и убывания функции.
Найдем вершину параболы
Тогда парабола убывает
Для наглядности смотри рисунок, ниже
1) Найдите нули функции,промежутки законопостоянства, промежутки возрастания и убывания функции
a) Нули функции
Раскроем модуль
и
т.е. число 2 и 4 -- ноли этой функции
б) Промежутки законопостоянства, для этого найдем
Тогда
Значит, в промежутке
в) Промежутки возрастания и убывания функции.
Функция убывает в промежутках (−∞; 3) и возрастает в промежутке (3;+∞). Смотри рисунок ниже
Приложения:

Похожие вопросы
Предмет: Другие предметы,
автор: tiktoker49
Предмет: Обществознание,
автор: ahmetshinemil116
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: svetlanayakovl
Предмет: География,
автор: katyusik056