Предмет: Алгебра,
автор: RainbowDash99
Решите, пожалуйста эти пять уравнений, думаю пять решений на 50 баллов - будет нормально, но не меньше решайте :с
Приложения:
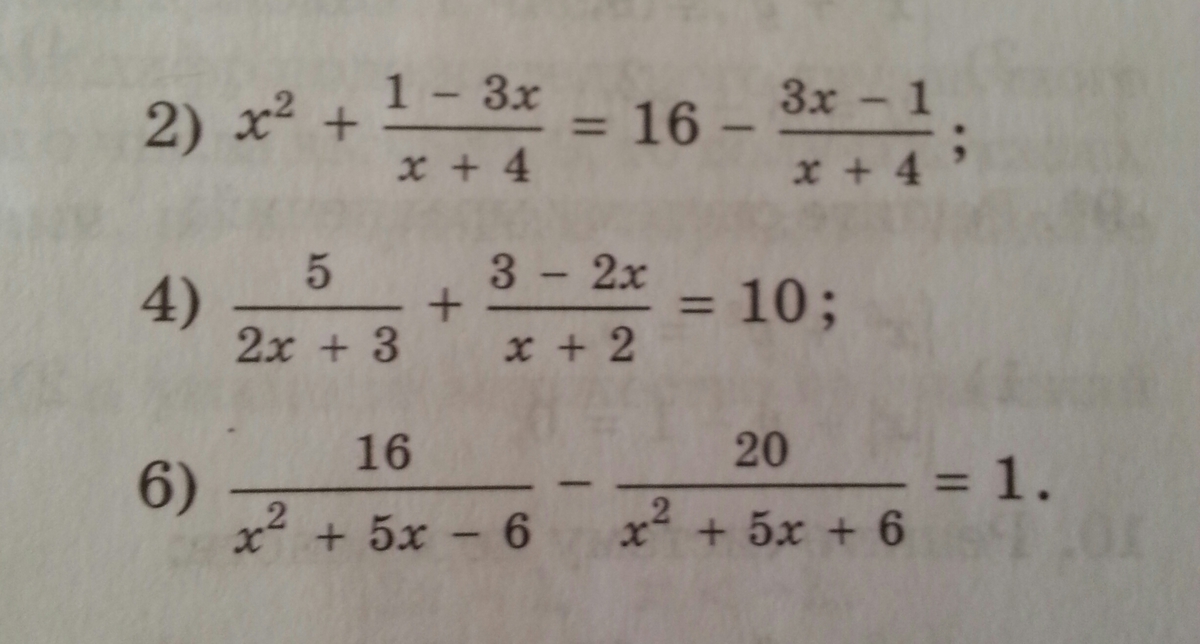
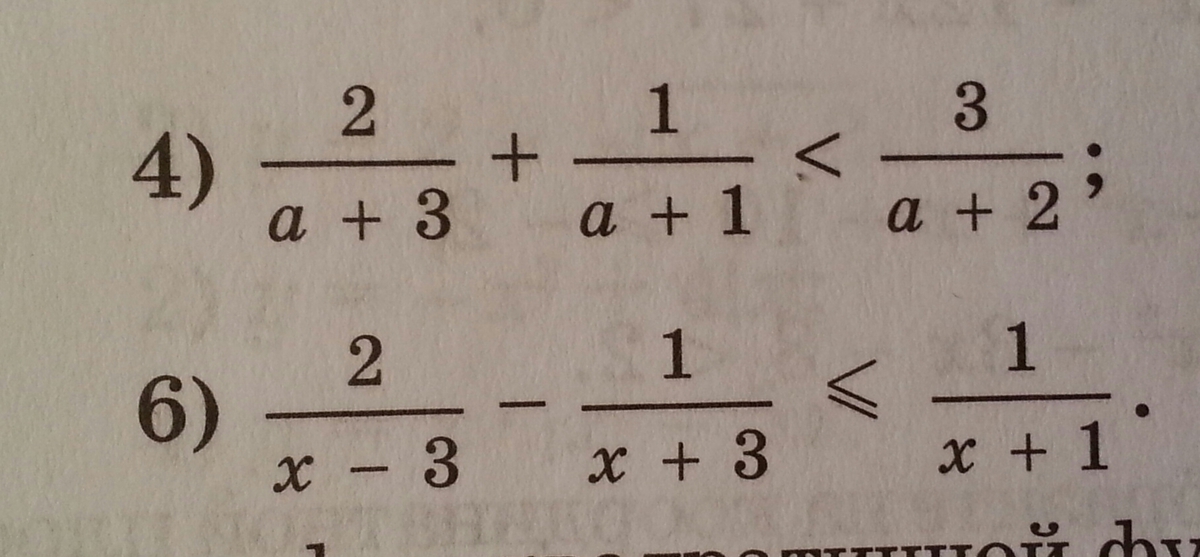
Ответы
Автор ответа:
0
Уравнения:
2)
Ответ: x=4.
4)
Ответ:
6)
Сделаем замену: a=x²+5x.
Проведём обратную замену.
Ответ: x={-7;2}.
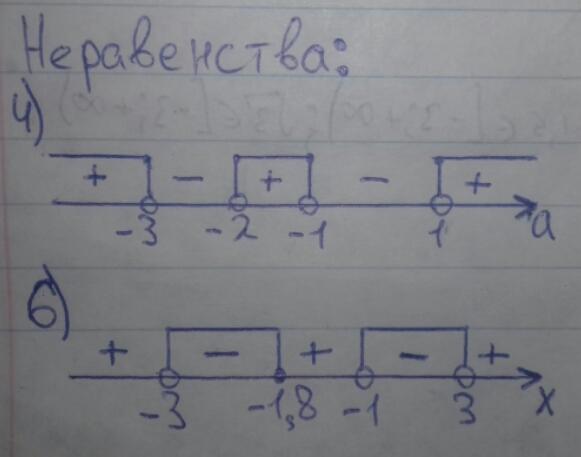
Неравенства:
4)
Ответ: a∈(-∞;-3)∪(-2;-1)∪(1;+∞).
6)
Ответ: x∈(-3;-1,8]∪(-1;3).
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: Hello12501
Предмет: Алгебра,
автор: Аноним
Предмет: Українська література,
автор: MarkFFomenko
Предмет: Математика,
автор: annazo2001