Question

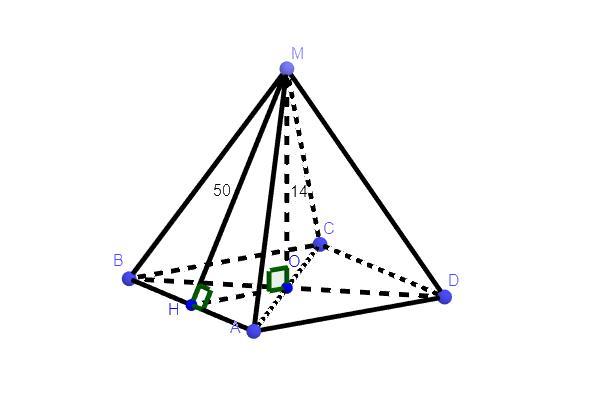
Точка М удалена от плоскости квадрата на 14см, а от каждой из его сторон на 50 см. Найдите сторону квадрата и расстояние от его вершин до точки М.

Answer 1

Дано: ABCD - квадрат

MO = 14 см

MH = 50 см

Найти: BM, AB

Так как расстояние от точки M до всех сторон квадрата одинаковое, следует, что ABCDM - правильная четырёхугольная пирамида

Проведём прямую OH

MO ⊥ ABCD ⇒ MO ⊥ OH

Рассмотрим ΔHMO - прямоугольный

По теореме Пифагора

$HO^2 = HM^2 - MO^2 \\HO = sqrt{(50-14)(50+14)} = sqrt{36*64} = 6 *8 = 48;cm$

AB = 2HO = 96 - сторона квадрата

Рассмотрим ΔABM - равнобедренный

MH - медиана ⇒ BH = 1/2 AB = 48

По теореме Пифагора

$BM^2 = BH^2 + HM^2\\BM^2 = 50^2+48^2\\BM = 2sqrt{1201};cm$