Предмет: Алгебра,
автор: locer
Решите, пожалуйста, желательно добавьте во вложении,
и объясните подробнее
Приложения:
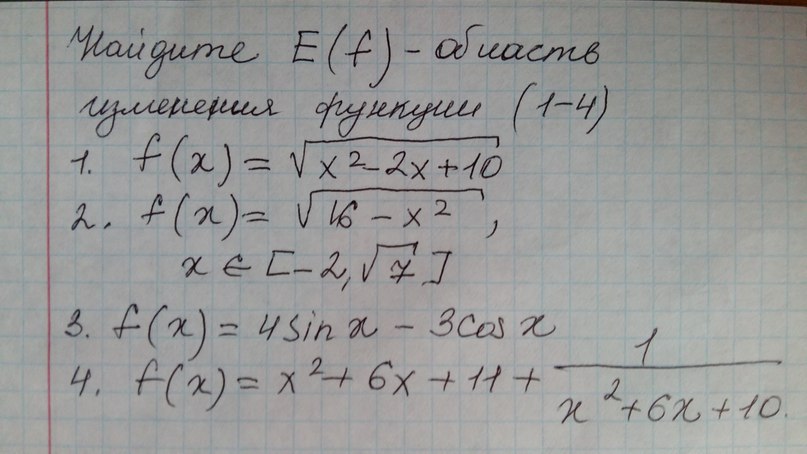
Ответы
Автор ответа:
0
1) 
При x = 1 будет f(x) = √9 = 3 - это минимальное значение.
Максимальное значение никак не ограничено.
E(f) = [3; +oo)
2)![f(x)= sqrt{16-x^2}; x=[-2; sqrt{7} ] f(x)= sqrt{16-x^2}; x=[-2; sqrt{7} ]](https://tex.z-dn.net/?f=f%28x%29%3D+sqrt%7B16-x%5E2%7D%3B+x%3D%5B-2%3B+sqrt%7B7%7D+%5D+)

Но
E(f)=[3; 4]
3)
Минимум будет при sin x = -1, тогда cos x = 0; f(x) = -4-3*0 = -4
Максимум будет при sin x = 1, тогда cos x = 0; f(x) = 4 - 3*0 = 4
E(f) = [-4; 4]
4)
При x = 3 будет f(x) = 0 + 2 + 1/(0 + 1) = 2 + 1 = 3
Максимальное значение никак не ограничено.
E(f) = [3; +oo)
При x = 1 будет f(x) = √9 = 3 - это минимальное значение.
Максимальное значение никак не ограничено.
E(f) = [3; +oo)
2)
Но
E(f)=[3; 4]
3)
Минимум будет при sin x = -1, тогда cos x = 0; f(x) = -4-3*0 = -4
Максимум будет при sin x = 1, тогда cos x = 0; f(x) = 4 - 3*0 = 4
E(f) = [-4; 4]
4)
При x = 3 будет f(x) = 0 + 2 + 1/(0 + 1) = 2 + 1 = 3
Максимальное значение никак не ограничено.
E(f) = [3; +oo)
Автор ответа:
0
Во-первых, я подозреваю, что они производную еще не проходили. А во-вторых, как из tg x = -4/3 получить f(x) = 5 ?
Автор ответа:
0
из tg x = -4/3 получилось, что максимум совсем НЕ при sin x = 1
Автор ответа:
0
Согласен, я ответил неправильно, но я все равно не понимаю, как решить эту задачу. А тем более, как ее решить БЕЗ производных.
Автор ответа:
0
во-первых, никто не запрещал применять производную --- задача не для 7 класса...
Автор ответа:
0
а ответ в любом случае должен быть правильным))
Похожие вопросы
Предмет: Математика,
автор: slavagroholo
Предмет: Математика,
автор: 21312344132
Предмет: Алгебра,
автор: sashastupcenko6
Предмет: Математика,
автор: narmalno