Предмет: Геометрия,
автор: Аноним
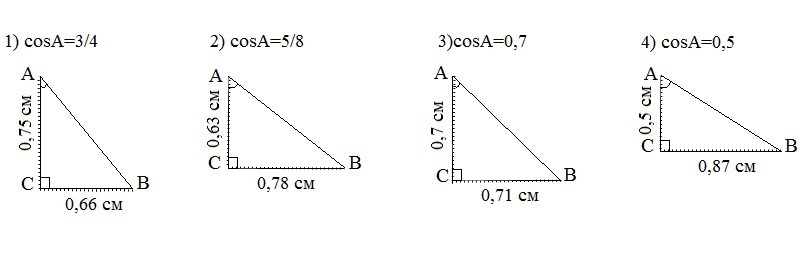
Нарисуйте прямоугольный треугольник, чтобы косинус острого угла был равен 1) 3/4; 2) 5/8; 3) 0,7; 4) 0,5
Ответы
Автор ответа:
0
Пусть дан треугольник АВС, где угол С=90°, АС и ВС - катеты, АВ - гипотенуза.
1) cosA=3/4. Исходя из определения косинуса острого угла cosA=АС/АВ (рис. треугольников во вложении), а синус острого угла sinA=ВС/АВ, т.е
АС/АВ=3/4, АС=3/4*АВ
 , т.е.
, т.е.
 ;
;  .
.
Для удобства расчетов примем здесь и далее АВ= 1см, тогда
АС=3/4*АВ=3/4*1=0,75 см; ≈0,66 см
≈0,66 см
Далее считаем аналогично
2) cosA=5/8
АС=5/8*АВ=0,625≈0,63 см

 ≈0,78 см
≈0,78 см
3) cosA=0,7
АС=0,7*АВ=0,7 см

 ≈0,71 см
≈0,71 см
4) cosA=0,5
АС=0,5*АВ=0,5 см

 ≈0,87 см
≈0,87 см
1) cosA=3/4. Исходя из определения косинуса острого угла cosA=АС/АВ (рис. треугольников во вложении), а синус острого угла sinA=ВС/АВ, т.е
АС/АВ=3/4, АС=3/4*АВ
Для удобства расчетов примем здесь и далее АВ= 1см, тогда
АС=3/4*АВ=3/4*1=0,75 см;
Далее считаем аналогично
2) cosA=5/8
АС=5/8*АВ=0,625≈0,63 см
3) cosA=0,7
АС=0,7*АВ=0,7 см
4) cosA=0,5
АС=0,5*АВ=0,5 см
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: MinAri09
Предмет: Математика,
автор: MoxinaAlmamadova
Предмет: Математика,
автор: mgfater
Предмет: Литература,
автор: Аноним