Предмет: Алгебра,
автор: MarMaLade
Алгебра, 9 класс. Помогите решить двойные неравенства.
А еще лучше, объясните, как это чудо чудное решается.
Приложения:
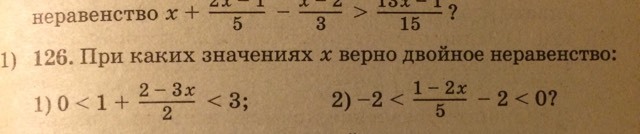
Ответы
Автор ответа:
0
1) 0< 1+(2-3x)/2 <3 .⇔0<2+(2-3x) <6 .⇔0<4-3x) <6 .⇔ -6 <3x -4 <0. ⇔
-6 +4 <3x < 4 .⇔ -2 <3x < 4 . ⇔ -2/3 < x < 4/3 . или иначе x∈(-2/3 ; 4/3).
2) -2< (1-2x)/ 5 -2 < 2 ; * * * +2 * * *
-2 +2< (1-2x)/ 5 < 2+2 ;
0<1-2x)/ 5 <4 ;
0<1-2x) <20 ; * * * умножаем на 5 * * *
- 20 <2x -1<0 ; * * * умножаем на (-1) * * *
-20 +1 <2x<1 ;
-19<2x<1 ;
-19/2 < x< 1 /2 или иначе x∈(- 9,5 ; 0,5).
-6 +4 <3x < 4 .⇔ -2 <3x < 4 . ⇔ -2/3 < x < 4/3 . или иначе x∈(-2/3 ; 4/3).
2) -2< (1-2x)/ 5 -2 < 2 ; * * * +2 * * *
-2 +2< (1-2x)/ 5 < 2+2 ;
0<1-2x)/ 5 <4 ;
0<1-2x) <20 ; * * * умножаем на 5 * * *
- 20 <2x -1<0 ; * * * умножаем на (-1) * * *
-20 +1 <2x<1 ;
-19<2x<1 ;
-19/2 < x< 1 /2 или иначе x∈(- 9,5 ; 0,5).
Автор ответа:
0
спасибо
Автор ответа:
0
я решал не -2< (1-2x)/ 5 -2 < 0 , а -2< (1-2x)/ 5 -2 < 0
Автор ответа:
0
идея следующая:
ко всем (трем) частям неравенства можно прибавить (вычесть) одно и то же число...
всем (три) части неравенства можно умножить (разделить) на одно и то же, не равное нулю, число...
т.е. можно делать все действия, что и с обычными (не двойными) неравенствами...
ко всем (трем) частям неравенства можно прибавить (вычесть) одно и то же число...
всем (три) части неравенства можно умножить (разделить) на одно и то же, не равное нулю, число...
т.е. можно делать все действия, что и с обычными (не двойными) неравенствами...
Приложения:
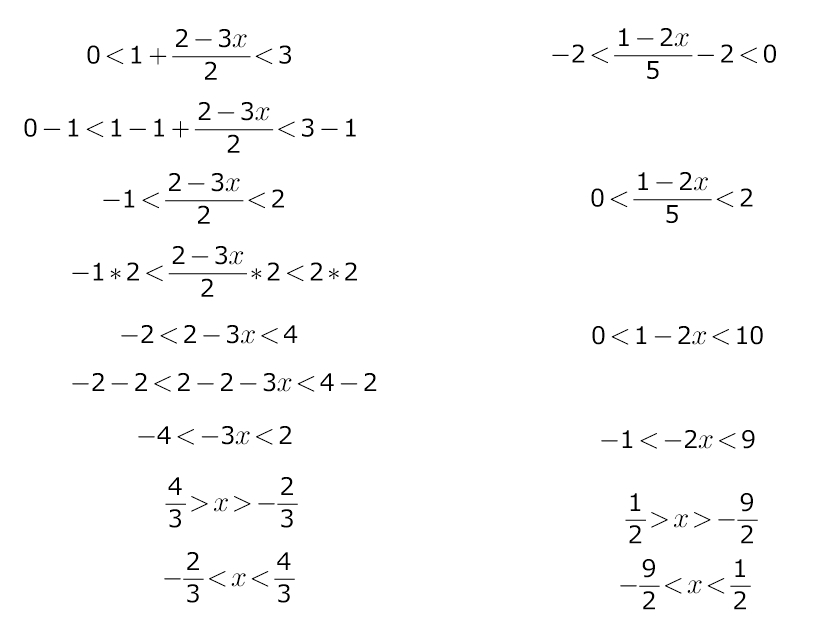
Автор ответа:
0
спасибо
Похожие вопросы
Предмет: Обществознание,
автор: lexal200koch
Предмет: Математика,
автор: aanakuanys108
Предмет: Українська мова,
автор: kunak81
Предмет: Математика,
автор: vipmiss55
Предмет: Геометрия,
автор: farakarad