Предмет: Алгебра,
автор: kovalskaya98
решите пожалуйста срочно надо!!!!
Приложения:
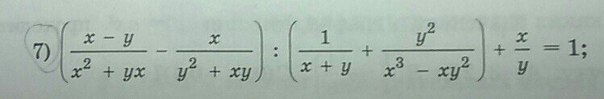
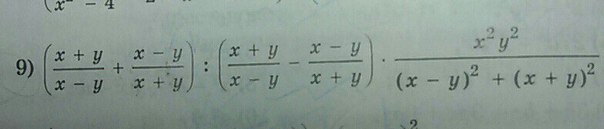
Ответы
Автор ответа:
0
7)

9)


9)
Похожие вопросы
Предмет: Геометрия,
автор: xolmatovbobur2
Предмет: Биология,
автор: NightHelp
Предмет: Математика,
автор: Аноним
Предмет: Литература,
автор: 690653
Предмет: Математика,
автор: oksanamotina