Предмет: Алгебра,
автор: Kwyuri1
А) найдите разность, девятый член и значение суммы первых десяти членов арифметической прогрессии 3,2;4,4,8;...
Б) найдите седьмой член и значение суммы первых двадцати членов арифметической прогрессии 40;39,6;39,2;...
В) шестой член арифметической прогрессии равен 35, а значение суммы первых восьми членов равно 220. Найдите первый член и разность прогрессии;
Г) значение суммы второго и восьмого членов геометрической прогрессии равно -60 , разность третьего и седьмого равно -40. Найдите первый член прогрессии.
Ответы
Автор ответа:
0
А) Дана арифметическая прогрессия: 3,2 ; 4 ; 4,8 ; ....
Разность: d = a₂ - a₁ = 4 - 3,2 = 0,8
Девятый член: а₉ = а₁ + d•(9 - 1) = 3,2 + 0,8•8 = 3,2 + 6,4 = 9,6
Значение суммы первых десяти членов: S₁₀ = (a₁ + a₁₀)•10/2 = (3,2 + 3,2 + 0,8•9)•5 = 13,6•5 = 68
Б) Дана ариметическая прогрессия: 40 ; 39,6 ; 39,2 ; ....
Разность: d = 39,6 - 40 = - 0,4
Седьмой член: а₇ = а₁ + d•(7 - 1) = 40 - 0,4•6 = 40 - 2,4 = 37,6
Значение суммы первых двадцати членов: S₂₀ = (a₁ + a₂₀)•20/2 = (40 + 40 - 0,4•19)•10 = 72,4•10 = 724
B) Дана арифметическая прогрессия:
Значение суммы первых восьми членов: S₈ = (a₁ + a₈)•8/2 = 220 ⇒ a₁ + a₈ = 55 ⇒ а₁ + (а₁ + d•7) = 55 ⇒ 2a₁ + 7d = 55 (1)
Шестой член: а₆ = 35 ⇒ a₁ + 5d = 35 (×2) ⇒ 2a₁ + 10d = 70 (2)
Отнимем из второго первое: (2) - (1)
2a₁ + 10d - (2a₁ + 7d) = 70 - 55 ⇒ 3d = 15 ⇒ d = 5 - разность
Первый член: а₁ + 5d = 35 ⇒ a₁ + 5•5 = 35 ⇒ a₁ = 10
Г) В условии данной задачи допущена ошибка: дана не геометрическая, а арифметическая прогрессия, в силу того что последнее уравнение четвёртой степени, которое приложено, просто не имеет корней.
Значение разности третьего и седьмого члена: а₃ - а₇ = - 40
(а₁ + 2d) - (a₁ + 6d) = - 40 ⇒ - 4d = - 40 ⇒ d = 10 - разность
Значение суммы второго и восьмого членов: а₂ + а₈ = - 60
(a₁ + d) + (a₁ + 7d) = - 60 ⇒ 2a₁ + 8d = - 60 ⇒ a₁ + 4d = - 30
Первый член: а₁ + 4•10 = - 30 ⇒ а₁ = - 70
Приложения:



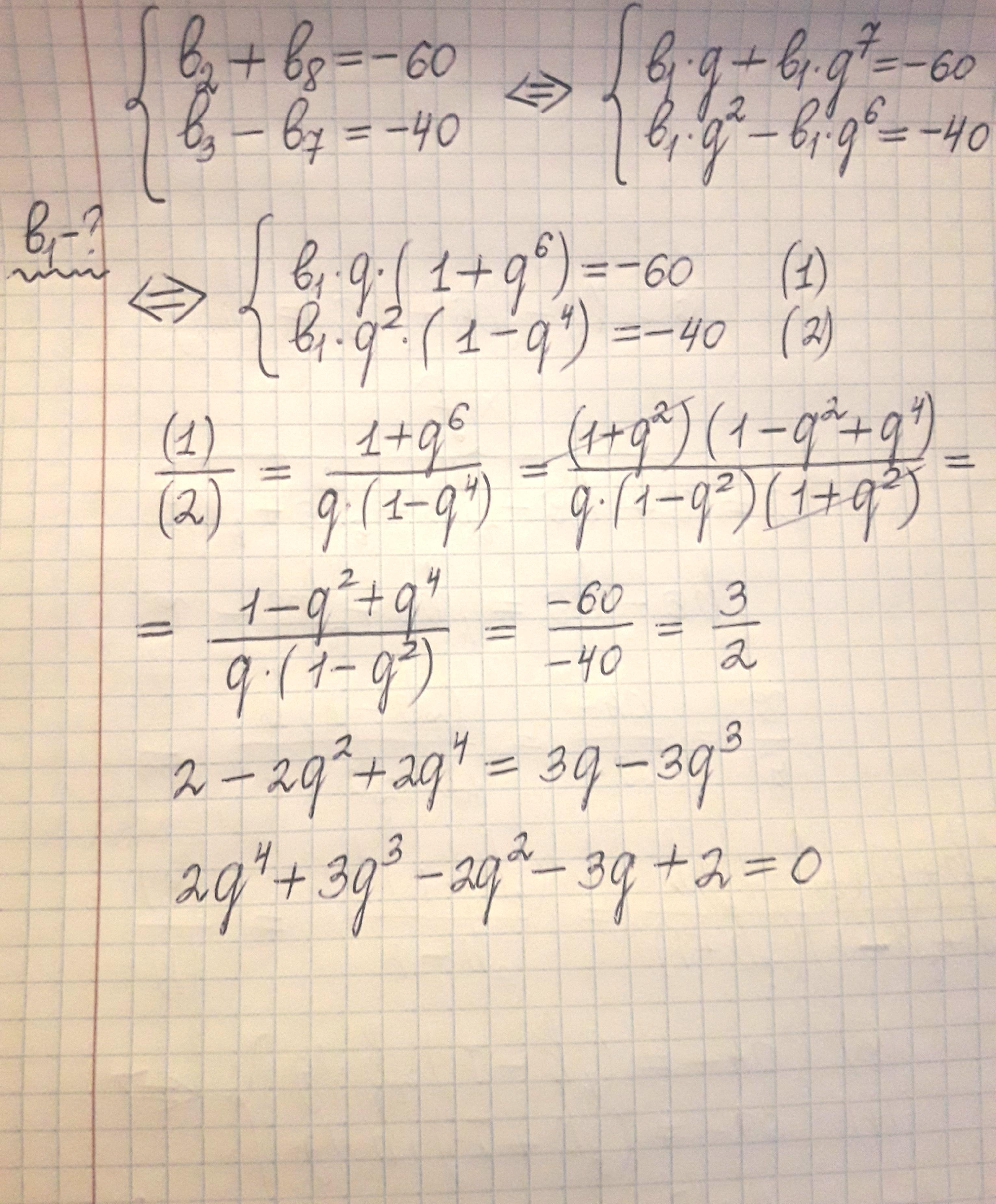
Похожие вопросы
Предмет: Биология,
автор: Sonechka571
Предмет: Математика,
автор: tahminadujseken
Предмет: Математика,
автор: arcenkova13
Предмет: Математика,
автор: kabalnovaalyona
Предмет: Биология,
автор: larayurevich