Question

В равнобедренном прямоугольном треугольнике один из катетов лежит в плоскости a, а другой образует с ней угол 45. Найдите угол между гипотенузой данного треугольника и данной плоскостью.
Если не трудно,с рисунком пожалуйста

Answer 1

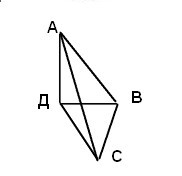
Равнобедренный прямоугольный ΔАВС (∠В=90°, АВ=ВС)
Опустим перпендикуляр на плоскость АД (∠АДВ=∠АДС=90°)
∠АВД=45°
Нужно найти ∠АСД.
В ΔАВС обозначим АВ=ВС=х, тогда гипотенуза АС=√2АВ²=√2х²=х√2
В прямоугольном ΔАДВ ∠АВД=45°, значит и ∠ВАД=45°, следовательно этот треугольник равнобедренный (АД=ВД=АВ/√2=х/√2).
Из прямоугольного ΔАДС найдем ∠АСД:
sin АСД=АД/АС=х/√2:х√2=1/2
∠АСД=30°