Question

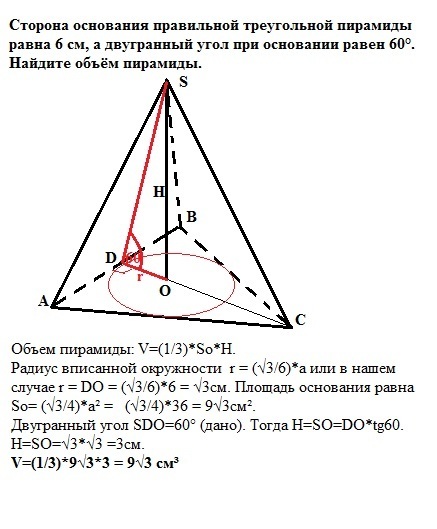
Сторона основания правильной треугольной пирамиды равна 6 см, а двугранный угол при основании равен 60 градусов. Найдите объём пирамиды

Answer 1

Объем пирамиды: V=(1/3)*So*H.

Радиус вписанной окружности правильного треугольника (основания) r=(√3/6)*a или в нашем случае r = DO = (√3/6)*6 = √3 см. Площадь основания равна So= (√3/4)*a² = (√3/4)*36 = 9√3см².

Двугранный угол SDO=60° (дано). Тогда из прямоугольного треугольника имеем: H=SO=DO*tg60. tg60 = √3. Тогда Н=SO=√3*√3 =3см.

V=(1/3)*9√3*3 = 9√3 cм³