Предмет: Алгебра,
автор: Аноним
Исследуйте количество неотрицательных корней уравнения х квадрат - (3-а)х + а квадрат - 9=0 в зависимости от параметра а
Ответы
Автор ответа:
0
условие существования корней: D >= 0
D = (3-a)² - 4*(a² - 9) = 9-6a+a²-4a²+36 = -3a² - 6a + 45 >= 0
a² + 2a - 15 <= 0
корни по т.Виета (-5) и (3)
парабола, ветви вверх, решение между корнями
-5 <= a <= 3 корни существуют при этих значениях (а)
для а = -5 и а = 3 корень ОДИН
корни по условию должны быть неотрицательны
см.файл
итого: для -5 < a <= -3 --- ДВА неотриц.корня
для a=-5 и -3 < a <= 3 ---ОДИН неотриц.корень
для всех остальных (а) корней НЕТ.
D = (3-a)² - 4*(a² - 9) = 9-6a+a²-4a²+36 = -3a² - 6a + 45 >= 0
a² + 2a - 15 <= 0
корни по т.Виета (-5) и (3)
парабола, ветви вверх, решение между корнями
-5 <= a <= 3 корни существуют при этих значениях (а)
для а = -5 и а = 3 корень ОДИН
корни по условию должны быть неотрицательны
см.файл
итого: для -5 < a <= -3 --- ДВА неотриц.корня
для a=-5 и -3 < a <= 3 ---ОДИН неотриц.корень
для всех остальных (а) корней НЕТ.
Приложения:
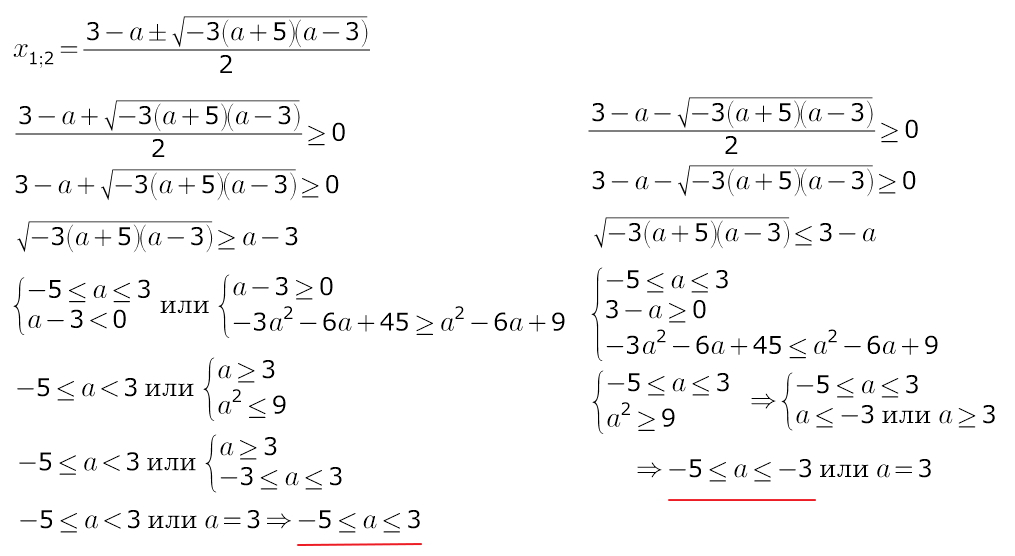
Автор ответа:
0
спасибо огромнейшее. вы супер
Автор ответа:
0
рада была помочь...
Похожие вопросы
Предмет: Русский язык,
автор: medvedevapolina2019
Предмет: Другие предметы,
автор: kkirilenko
Предмет: Русский язык,
автор: lera94361
Предмет: Математика,
автор: CathyRey
Предмет: Математика,
автор: sherbinina1978