Предмет: Геометрия,
автор: grishinnik77
помогате пожалуйста решить задачу по геометрии (в равнобедренной трапеции периметр равен 64 см разность оснований равна 18 см а высота относится к боковой стороне как 4:5. найдите площадь трапеции. найдите площадь квадрата, диагональ которая равна 6 см )
Ответы
Автор ответа:
0
Пусть дана трапеция АВСD,
высота ВН.
АВ=5а,
ВН=4а
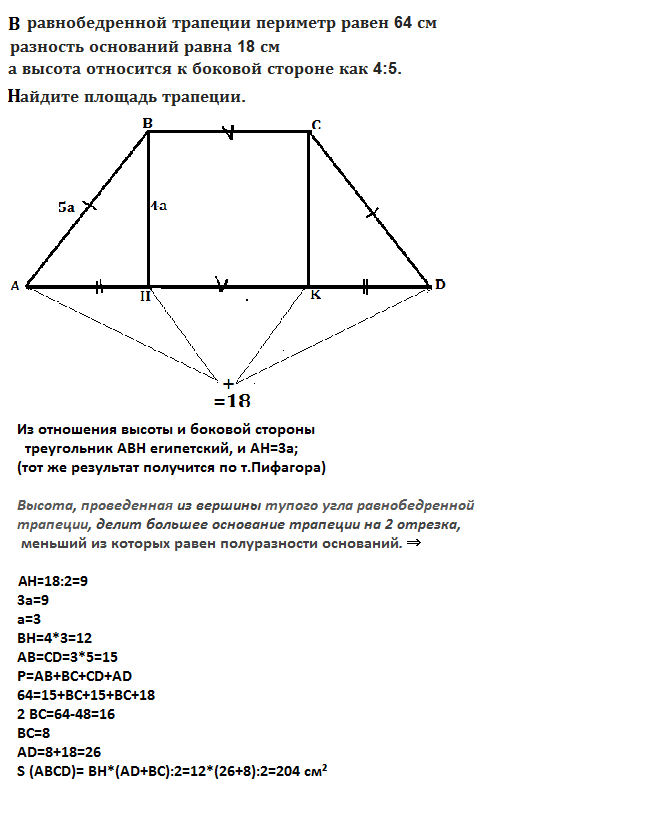
Из отношения высоты и боковой стороны треугольник АВН египетский, и АН=3а; тот же результат получится по т.Пифагора.
Высота, проведенная из вершины тупого угла равнобедренной трапеции, делит большее основание трапеции на 2 отрезка, меньший из которых равен полуразности оснований. ⇒
АН=18:2=9
3а=9
а=3
ВН=4*3=12
АВ=СD=3*5=15
P (ABCD)=AB+BC+CD+AD
64=15+BC+15+BC+18
2 BC=64-48=16
BC=8
AD=8+18=26
S (ABCD)= BH*(AD+BC):2=12*(26+8):2=204 см²
-----------------------
Площадь ромба равна половине произведения его диагоналей.
Квадрат - ромб.
S=d²:2=6²:2=18 см²
высота ВН.
АВ=5а,
ВН=4а
Из отношения высоты и боковой стороны треугольник АВН египетский, и АН=3а; тот же результат получится по т.Пифагора.
Высота, проведенная из вершины тупого угла равнобедренной трапеции, делит большее основание трапеции на 2 отрезка, меньший из которых равен полуразности оснований. ⇒
АН=18:2=9
3а=9
а=3
ВН=4*3=12
АВ=СD=3*5=15
P (ABCD)=AB+BC+CD+AD
64=15+BC+15+BC+18
2 BC=64-48=16
BC=8
AD=8+18=26
S (ABCD)= BH*(AD+BC):2=12*(26+8):2=204 см²
-----------------------
Площадь ромба равна половине произведения его диагоналей.
Квадрат - ромб.
S=d²:2=6²:2=18 см²
Приложения:
Автор ответа:
0
спасибо большое
Похожие вопросы
Предмет: Русский язык,
автор: egorzhukov5v
Предмет: Биология,
автор: nokard8
Предмет: География,
автор: bihszjrpeqzx
Предмет: Математика,
автор: Mnekau
Предмет: Математика,
автор: odessa2005