Предмет: Геометрия,
автор: djulietta
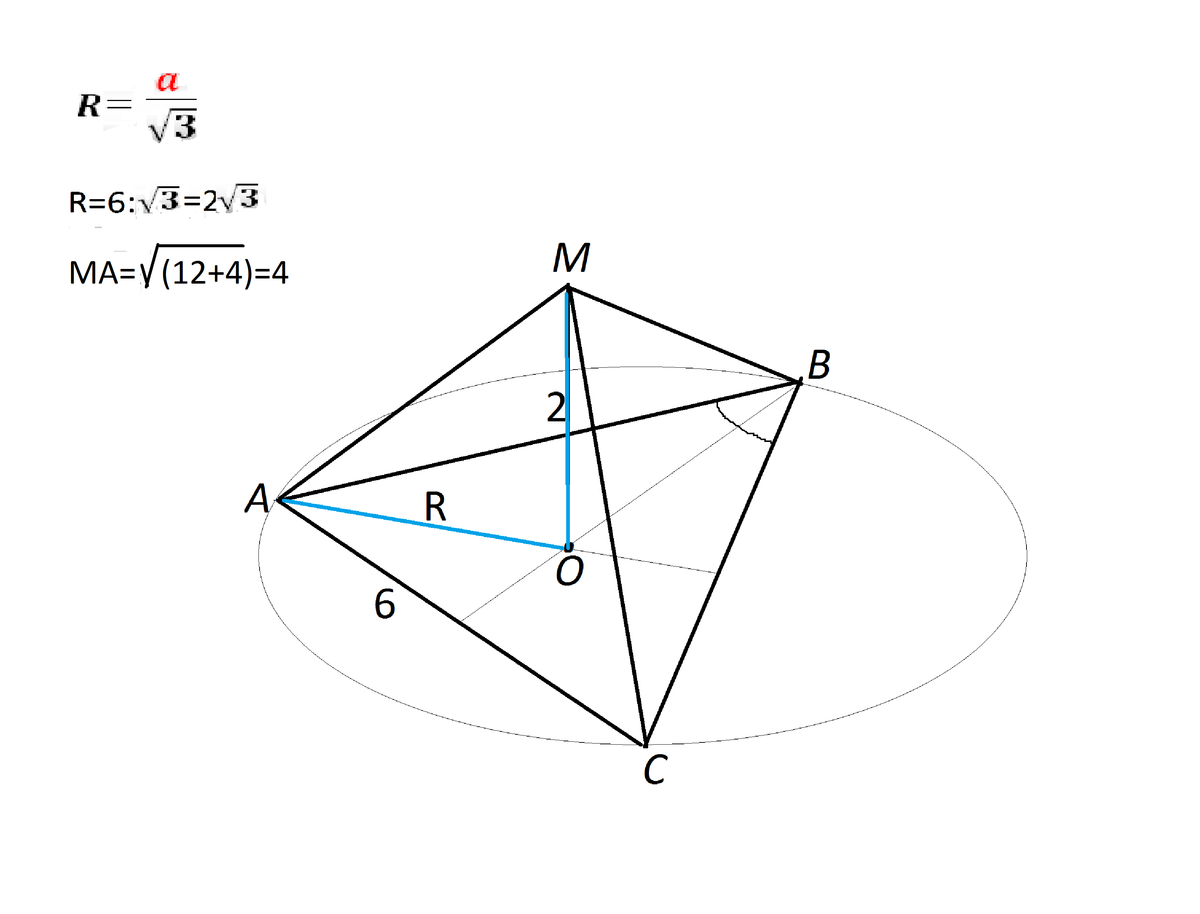
Треугольник ABC правильный. Точка O -его центр. Прямая OM перпендикулярна плоскости ABC. Докажите, что MA=MB=MC. Найдите MA, если AB=6см, MO=2см
Ответы
Автор ответа:
0
Центр правильного треугольника - это центр описанной и вписанной окружности, и расположен он в точке пересечения высот (медиан, биссектрис).
Т.к. все высоты правильного треугольника равны между собой, эта точка делит каждую высоту ( медиану) этого треугольника по свойству медиан в отношении 2:1, считая от вершины , т.е.
АО=ВО=СО,
.Эти отрезки - проекции наклонных МА, МВ, МС
Поскольку проекции равны, то и наклонные равны. Т.е.
МА=МВ=МС
МА по т. Пифагора
МА=√ (АО²+МО²)
АО - радиус описанной окружности и может быть найден по формуле
R=a/√3
или найти длину высоты данного правильного треугольника, и 2 ее трети и будут проекциями наклонных , т.е. равны АО.
h=a√3):2=6√3):2=3√3
AO=3√3):3)·2=2√3
МА=√(АО² + МО²)=√(12+4)=4 см
Т.к. все высоты правильного треугольника равны между собой, эта точка делит каждую высоту ( медиану) этого треугольника по свойству медиан в отношении 2:1, считая от вершины , т.е.
АО=ВО=СО,
.Эти отрезки - проекции наклонных МА, МВ, МС
Поскольку проекции равны, то и наклонные равны. Т.е.
МА=МВ=МС
МА по т. Пифагора
МА=√ (АО²+МО²)
АО - радиус описанной окружности и может быть найден по формуле
R=a/√3
или найти длину высоты данного правильного треугольника, и 2 ее трети и будут проекциями наклонных , т.е. равны АО.
h=a√3):2=6√3):2=3√3
AO=3√3):3)·2=2√3
МА=√(АО² + МО²)=√(12+4)=4 см
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: kimangelina166
Предмет: Английский язык,
автор: censorshipbb
Предмет: Алгебра,
автор: madelamebonu
Предмет: Математика,
автор: лумка