Предмет: Геометрия,
автор: laer300
Вокруг окружности описана прямоугольная трапеция, длины оснований которой равны 8 и 12. Найдите радиус данной окружности.
Ответы
Автор ответа:
0
Вокруг окружности можно описать четырехугольник тогда и только тогда, когда суммы его противоположных сторон равны.
Трапеция АВСD - четырехугольник. ⇒
АD+BC=AB+CD
АD+BC=20
AB+CD=20
Пусть АВ=х.
Тогда
CD=20-x⇒
Опустим из С высоту на большее основание и получим треугольник СНD,
в котором НD=12-8=4
CH=AB=x
CD=20-x
По т.Пифагора
НD²=CD²=CH²
16=400-40x+x²-x²
40x=384
x=9,6
Высота трапеции равна диаметру вписанной в нее окружности.
D=9,6
r=9,6:2=4,8
Трапеция АВСD - четырехугольник. ⇒
АD+BC=AB+CD
АD+BC=20
AB+CD=20
Пусть АВ=х.
Тогда
CD=20-x⇒
Опустим из С высоту на большее основание и получим треугольник СНD,
в котором НD=12-8=4
CH=AB=x
CD=20-x
По т.Пифагора
НD²=CD²=CH²
16=400-40x+x²-x²
40x=384
x=9,6
Высота трапеции равна диаметру вписанной в нее окружности.
D=9,6
r=9,6:2=4,8
Приложения:
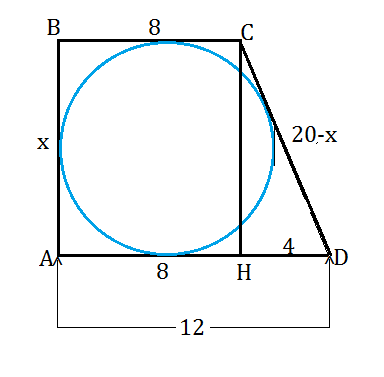
Похожие вопросы
Предмет: Українська мова,
автор: offisialangelina204a
Предмет: История,
автор: fjfudbxhrbd
Предмет: Алгебра,
автор: malaya1602
Предмет: Химия,
автор: r1p0
Предмет: Математика,
автор: SamirMuradogl